Following Apple and Signal, Zoom Now Moves To Post-Quantum Cryptography. Is Classical Cryptography Dying?

A Deep dive into how Classical Cryptography works, how powerful Quantum computers break it, how Post-quantum Cryptography works, and how it is being adapted swiftly to save the Internet.

Jun 04, 2024

I recently came across this blog post from Zoom that announced that it is now adopting Post-Quantum End-to-End Encryption for its Video Conferencing services.

It all started with Signal adapting the Post Quantum XDH (PQXDH) Key Agreement Protocol in 2023, becoming the first large-scale message app to do so.

This was soon followed by Apple adopting PQ3, a post-quantum cryptographic protocol for securing iMessage, in February 2024.

Finally, Zoom is now the first UCaaS (Unified Communications as a Service) company to adopt this security feature!

This means that from now on, users can ensure that their Zoom meetings are kept completely private and encrypted using advanced algorithms.

These algorithms make sure that apart from the participants of the meeting, no external parties, hackers or even Zoom itself, can gain access to the meeting content.

What’s special about these encryption algorithms is that even a Quantum computer cannot break them!

Zoom specifically used an algorithm called Kyber 768, which is being standardized by the National Institute of Standards and Technology (NIST), for this purpose.

This story is a curious exploration into what Encryption is, how End-to-end Encryption works, how Quantum computers break conventional encryption and how Post-quantum Cryptography might save our privacy and the Internet.

Let’s go!

But First, What Really Is Encryption?

Encryption is the technique of converting publically interpretable data or Plaintext into unreadable data or Ciphertext.

It is done to ensure that data remains confidential and can only be deciphered by someone who it is intended for.

In easy words, it is the art of keeping secrets, secrets.

We unknowingly use multiple sophisticated encryption techniques when we use the internet every day.

Everything that we type in and request through our browser is kept secret using these techniques so that a third person cannot eavesdrop on what we are up to on the internet.

How Is Encryption Made Possible?

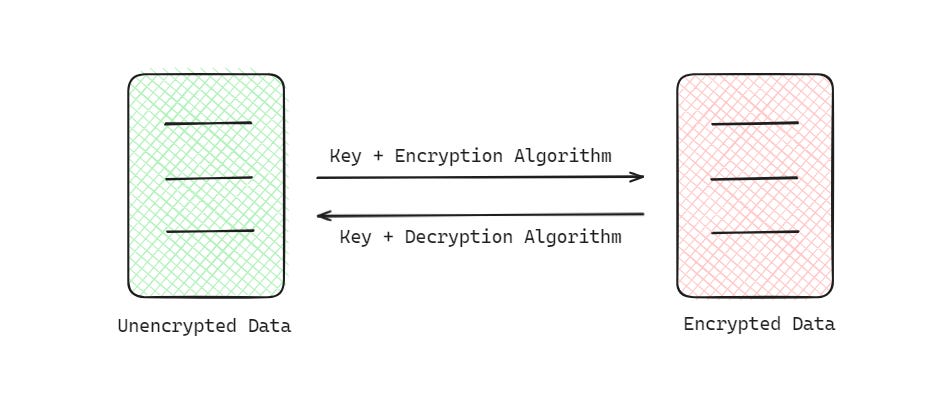
Encryption uses two key (no pun intended) elements —

Key(s)
An encryption/decryption algorithm that uses this key to encrypt or decrypt data

Based on how many keys are used in the process, the techniques are divided into —

Symmetric Encryption — where the same key is used to encrypt and decrypt the data

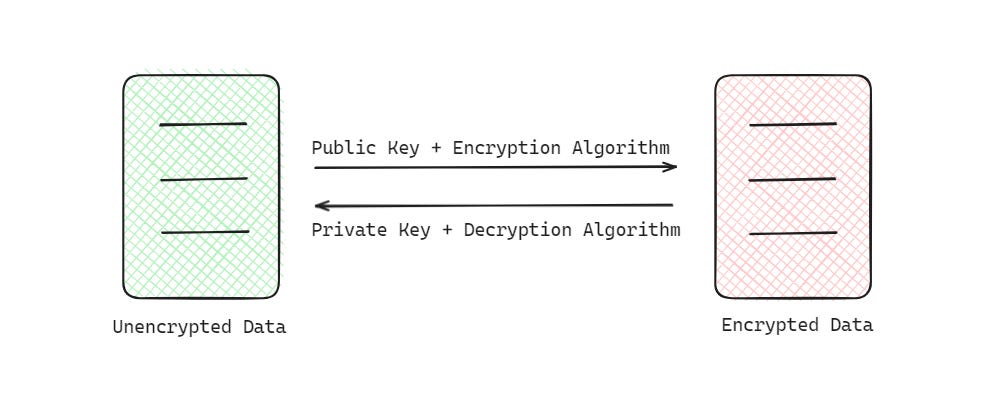
**Symmetric Encryption** (Image created by author)

2. Asymmetric Encryption — where a pair of keys namely, Public key and Private key are generated and are used to encrypt and decrypt data, respectively.

Asymmetric encryption is therefore also called Public Key Encryption.

Symmetric Encryption

Some examples of Symmetric Encryption algorithms are —

These algorithms use a series of mathematical operations (such as Bit shifts, Substitutions, Permutations and Logical gate operations) to jumble up the input using a key, during the Encryption process.

These operations are quick and use small key sizes. Therefore, these algorithms can encrypt large amounts of data very efficiently.

There’s a little downside to them too.

Because the same key is used to reverse these operations during the Decryption process, this key must be securely shared between users for the technique to work.

Asymmetric/ Public-Key Encryption

Some examples of Asymmetric Encryption algorithms are —

These algorithms rely on the difficulty of some mathematical operations that are easy to solve in one direction but are extraordinarily difficult to solve in the other.

The RSA algorithm is based on the fact that it is easy to multiply two prime numbers but it is impossible to factor large composite numbers into their prime factors.
The DSA algorithm is based on the difficulty of the Discrete Logarithm Problem i.e. —

Given a prime number p, a generator value g and a number y in a Finite group, where y = g^x mod p , it is extremely easy to compute y but the reverse process of finding x, given p,g and y is extremely tough.

The ECC algorithm is based on the difficulty of the Elliptic Curve Discrete Logarithm Problem i.e. —

Given an elliptic curve E defined by an equation y² = x³ + ax + b (where a and b are constants in a Finite field), for two points on the curve P and Q where Q = kP, it is extremely difficult to find k, given the value of these points.

(Here’s a post where I’ve described ECC in detail if you’re curious about it.)

These mathematical operations are usually computationally intensive and lead to larger key sizes as compared to the Symmetric Encryption ones.

But the best part about these is that two keys (Public and Private) are generated in the process.

The Public key, which is used to encrypt data, can be shared openly.

The users have to just keep their Private key, the one used to decrypt data, safe and hidden.

How Are We Kept Secure When Browsing The Internet?

Symmetric and Asymmetric algorithms are usually used together, and these form the basis of security on the Internet.

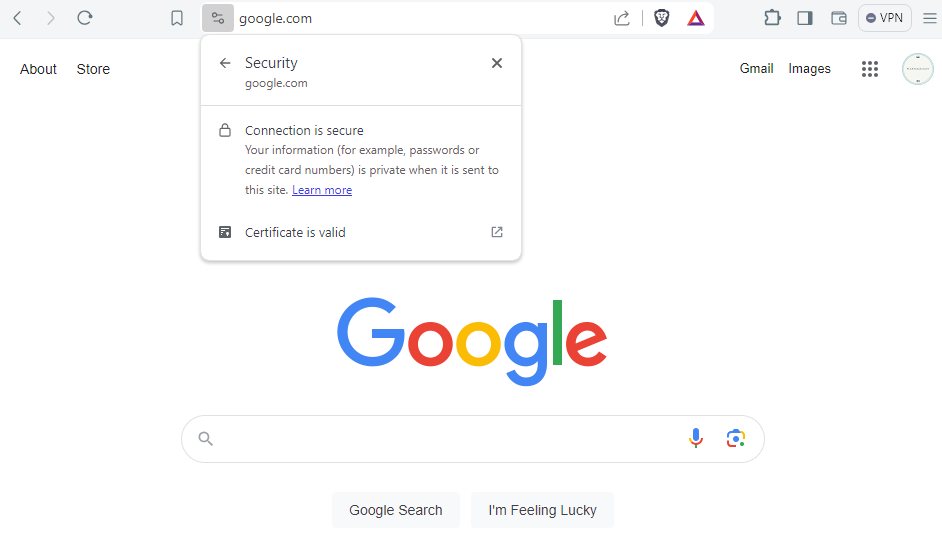
Have you ever noticed that little lock icon when you access a website?

TLS securing my connection with Google’s servers (Screenshot by author)

That little lock icon tells that a protocol called Transport Layer Security (TLS) is being used to encrypt the data between your browser and a website’s server.

This protocol ensures that there is no eavesdropping on your connection and the transferred data cannot be tampered with on the way.

Apart from being used by web browsers, it also secures other applications such as email, instant messaging, and voice-over IP.

The latest version of TLS i.e. 1.3 uses a combination of different cryptographic algorithms which in short are described using a Cipher Suite.

One of them recommended by the National Cyber Security Centre of the U.S. is TLS_AES_128_GCM_SHA256.

This TLS Cipher suite uses asymmetric algorithms like Elliptic-curve Diffie-Hellman (to generate shared keys) and Elliptic Curve Digital Signature Algorithm (to authenticate users) to establish a secure connection over the insecure internet.

Then, it uses Advanced Encryption Standard (AES) in Galois/Counter Mode, a fast symmetric algorithm to encrypt data to send over the secure network.

Alongside this, the SHA256 hashing algorithm is used to elevate the security in the intermediate steps of this process.

How Is Messaging Kept Secure With Encryption?

Have you ever noticed the header on your WhatsApp chats that tells that all your messages are end-to-end encrypted?

End-to-end encryption (E2EE) means that all the messages between the communicating users are kept secure and private, and no other user including WhatsApp can read these messages.

Many modern messaging platforms like WhatsApp and Signal use E2EE.

This ensures the prevention of active eavesdropping over our data — an attack called the Man-in-the-middle attack.

Both WhatsApp and Signal use the same end-to-end encryption protocol called the Signal Protocol (written primarily in Rust) developed by Open Whisper Systems.

This protocol again uses both symmetric and asymmetric algorithms, and a particularly interesting one of them is the Double Rachet Algorithm which allows two parties to exchange encrypted messages based on a shared secret key.

How Secure Are The Conventional Cryptographic Algorithms?

Let’s take an algorithm such as AES (Advanced Encryption Standard) with a key size of 256 bits.

This means that 2²⁵⁶ possible keys can be generated when using it.

This is a 78-digit long number, that is larger than the age of the universe and the number of atoms in the observable universe.

Even with a supercomputer that tries to guess a secret key at a speed of a trillion (10¹²) keys per second, it would take years 1.16 × 10⁵⁸ years to do so.

(Note that the age of the universe is just 1.38 × 10¹⁰ years.)

Amazing! So what’s the problem with conventional cryptography then?

The answer — Quantum computers are coming to break it all.

What Are Quantum Computers & Why Are Cryptographers Scared Of Them?

Quantum computers are a completely different type of computing model that works on the principles of Quantum Mechanics.

While classical computers use Bits (0 and 1) to represent data, quantum computers use Qubits that can exist in a state of both 0 and 1 at the same time (a property called Quantum Superposition).

This allows a Quantum computer to process a vast number of data values simultaneously.

Qubits can also be Entangled.

This means that the state of a qubit can be related to another however far they are kept from each other.

The information between such entangled qubits can be transmitted instantaneously regardless of the distance between them.

This property allows extremely fast information transfer and processing within a quantum computer.

Many clever minds have already worked on these quantum properties and proposed extremely efficient algorithms.

Grover Database Search algorithm, by Lov Kumar Grover, is one of them.

It tackles the problem of searching for an item in an unsorted database containing N items.

With a classical computer, doing this requires O(N) time, but with Grover’s algorithm, this can be done in O(N¹/²) time, or with a quadratic speedup over the classical algorithm of checking each item one at a time.

Another one by Peter Williston Shor, called Shor’s algorithm can factorize a composite number N into its prime factors.

The most efficient algorithm for factoring large integers today is the General Number Field Sieve (GNFS).

Its time complexity is shown as follows —

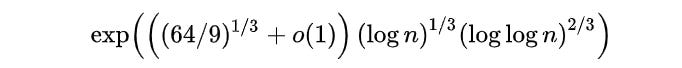
The time complexity of the **General number field sieve** for factoring an integer ’n’ (Image from Wikipedia)

Shor’s algorithm on the other hand has a time complexity of O((log N)³).

This is a superpolynomial boost-up when compared to the classical approach.

30 years after when Shor published this algorithm, Oded Regev in 2023, developed and published a multidimensional version of Shor’s algorithm that operates even faster.

Since asymmetric cryptography is based on the difficulty of factoring large prime numbers, algorithms like these, when used together, will completely break it.

To date, experiments have just been able to factor 21 as the largest integer, but companies are building Quantum computers at a fast pace.

At present, the largest Quantum computer developed by Atom consists of 1,225 Qubits. A close competitor is IBM’s Condor, a 1,121-Qubit quantum computer.

According to researchers, we still need millions of qubits to break algorithms like RSA and DSA, but we are quickly reaching there.

(Here’s a roadmap from IBM that demonstrates how they plan to achieve full-capacity quantum supercomputers beyond 2033.)

Even when we do not have powerful enough quantum computers today, malicious entities are storing large amounts of encrypted data to break them at a later day when they have access to quantum computers.

This is an attack termed — ‘Harvest Now, Decrypt Later’.

(A random fact btw — the date when quantum computers will beat public-key cryptography is called Y2Q or Q-Day.)

So, should we be scared?

Not really! Cryptographers from all around the world have our back.

Here Comes Post Quantum Cryptography (PQC)

In 2017, the National Institute of Standards and Technology (NIST), went through 82 submissions that were extensively evaluated in 3 rounds of intense scrutiny over 5 years.

In 2022, NIST announced a selection of 4 cryptographically secure algorithms out of these 82 algorithms, that cannot be broken down even with an advanced quantum computer.

For Asymmetric encryption, they selected an algorithm called CRYSTALS-Kyber.

The other three algorithms were selected for creating Digital Signatures.

(CRYSTALS stands for Cryptographic Suite for Algebraic Lattices.)

These algorithms rely on mathematical problems that are extremely challenging to solve using quantum and classical computers.

Here are those problems —

CRYSTALS-Kyber: Module Learning With Errors (Module-LWE)
CRYSTALS-Dilithium: Module Learning With Errors (Module-LWE) and Module Short Integer Solution (M-SIS) problem
FALCON: Short Integer Solution (SIS) problem over NTRU (N-th Degree Truncated Polynomial Ring Units) Lattices
SPHINCS+: based on Stateless Hash-Based Signatures

Since Signal, Apple and Zoom rely on Kyber, we will focus on it and dive deep into how it works.

A Deep Dive Into CRYSTALS-Kyber

Kyber is an IND-CCA2-secure Key Encapsulation Mechanism (KEM).

IND-CCA2 stands for INDistinguishability under adaptive Chosen Ciphertext Attack.

In easy words, it means that an attacker even with the ability to decrypt chosen encrypted messages cannot tell the difference between different encrypted messages.

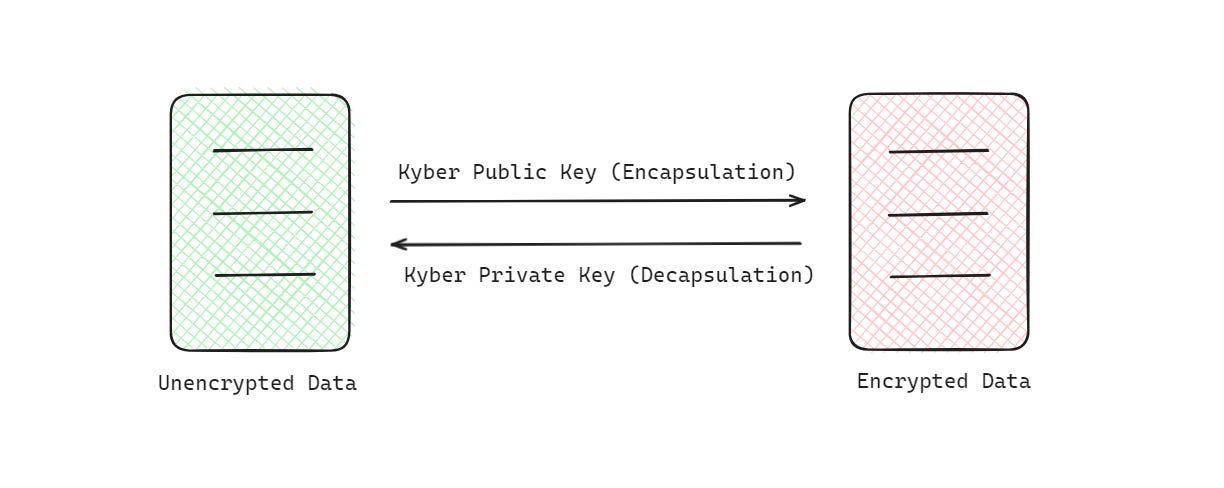
The Key Encapsulation Mechanism of Kyber has three basic steps—

Public & Private key Generation
Encapsulation i.e. generation of encrypted data using the Public key
Decapsulation i.e. decryption of data using Private key

(This is the same as what the classical Asymmetric encryption algorithms do.)

Kyber Encapsulation & Decapsulation (Image created by author)

Kyber’s three versions (with three different parameter sets) are roughly equivalent in security to the following versions of AES.

Kyber-512 ≈ AES-128
Kyber-768 ≈ AES-192
Kyber-1024 ≈ AES-256

It is mathematically based on the difficulty of solving the Learning-With-Errors (LWE) problem over Module Lattices.

To understand what a Module Lattice is, we first need to learn the definitions of Lattice, Ring, Field, Vector Space and Module.

What is a Lattice?

Firstly, a Lattice is a discrete non-overlapping set of points in Euclidean space that are arranged in a regular grid-like pattern.

Each point in a lattice is the sum of the integer multiples of the basis vectors.

Any point p in a lattice can be represented using the following equation:

p = a * v(1) + b * v(2) + ...

where a and b are integers, and v(1) and v(2) are the basis vectors.

Mathematically, a Lattice can be denoted as the following —

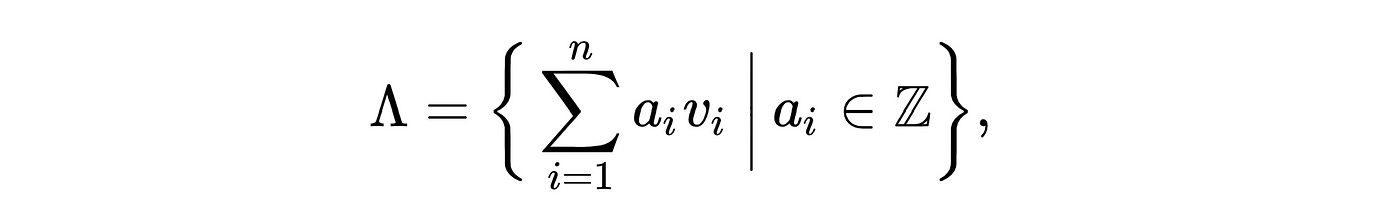
Definition of Lattice (Image from Wikipedia)

where:

v(1), v(2) .. v(i) are linearly independent basis vectors for i dimensions of Euclidean space
a(i)v(i) represents a point
a(i) is an integer
Z represents the set of integers

What is a Field?

A Field is a set of numbers on which addition, subtraction, multiplication, and division are defined.

These operations have the following properties:

Associativity
Commutativity
Distributivity
Identity Elements (Additive identity and Multiplicative identity)
Inverses (Additive inverse and Multiplicative inverse)

For example, the Field of Rational Numbers or Real numbers.

What is a Ring?

A Ring is a mathematical structure that generalises Fields.

In a Ring, multiplication need not be commutative and multiplicative inverses need not exist for all non-zero elements.

For example, in a Ring of integers, all other integers except 1 and -1 don’t have multiplicative inverses within the set of integers.

In a Ring of Polynomials, the coefficients come from a given Ring.

What is a Vector Space?

Vector space is a set of elements known as Vectors, which can be added and scaled by numbers known as scalars (Scalar multiplication).

What is a Module?

A Module is a generalization of a vector space where the scalars are taken from a Ring instead of a Field.

Finally — What is a Module Lattice?

A Module Lattice is a lattice that is also a Module over a Ring.

In easy words, a Module Lattice combines the properties of both a Lattice and a Module.

Now that we know about this mathematical structure, let’s learn about the Learning With Errors (LWE) problem.

What is Learning With Errors (LWE)?

Consider the following two linear equations.

2x + 3y = 7 4x − y = 5

These can be easily solved using simple algebraic techniques to obtain x = 11/7 and y = 9/7.

Next, let’s add some noise/ error to these equations.

2x + 3y + e(1) = 7 4x − y + e(2) = 5

where e(1) = 1 and e(2) = -1.

After adding the errors, these noisy equations look like the following —

2x + 3y = 6 4x − y = 6

When we solve these equations, we obtain x = 12/7 and y = 6/7.

This result is very different from the previous one and this is what the Learning with Errors problem is.

It is based on the idea of representing secret information as a set of linear equations with errors/ noise.

This secret information is usually a high-dimensional vector that when added noise to, cannot be recovered even using advanced quantum computers.

The LWE problem can be mathematically stated as —

Given a matrix A and a secret vector s along with a noise vector e, the LWE problem is about finding s from the result vector b in the following linear equation.
A * s + e = b

What is Module- LWE?

Module-LWE is the generalisation of the LWE problem over Modules defined by Rings of Polynomials.

Kyber is based on this hard-to-solve M-LWE problem.

This variant of LWE is used in Kyber because it offers efficient arithmetic operations, reduced key sizes, and a broader parameter choice, at the same time staying extremely tough to solve just like LWE.

The problem can be mathematically defined as follows —

Given a matrix A (whose values are polynomials from a Ring) and a secret vector of Polynomials s along with a noise vector of Polynomials e, the M-LWE problem is about finding s from the result vector b in the following linear equation.
A * s + e = b

In the context of Kyber, the tuple (A, b)represents the Public key and s represents the Private key.

The hardness of the M-LWE problem is based on a Lattice problem called the Shortest vector problem (SVP).

This problem goes like this —

Given a Lattice, find the non-zero lattice vector with the smallest Euclidean length.

Because, solving M-LWE is at least as hard as solving the hardest instances of SVP, which are considered computationally infeasible (by both classical and quantum computers), this provides a strong security foundation for Kyber.

How To Use Kyber?

The official Kyber website recommends using Kyber along with the established pre-quantum/ classical cryptographic algorithms.

The recommended version by the website is Kyber-768 because it achieves more than 128 bits of security against all known classical and quantum attacks.

This means that to break Kyber-768, one would require computational resources equivalent to performing 2¹²⁸ operations.

Kyber can be built using its public GitHub repository or one can use its implementation in liboqs, an open-source C library for quantum-safe cryptographic algorithms.

Some other third-party implementations of Kyber are mentioned here —

Implementation in Rust by Argyle Software
Implementation in Python by Dominik Klein
Implementation in Java by Steven Fisher
Implementation in Typescript by Steven Fisher
Implementation in Go by Yawning Angel
Implementation in JavaScript by Anton Tutoveanu

The US government along with many major companies like Amazon, Cloudflare, and IBM have already adopted Post-quantum cryptography.

This trend is being followed by public communication applications like iMessage, Signal and now Zoom.

Have you started familiarising yourself with this technology yet?

Let me know in the comments below.

Into AI

Discussion about this post