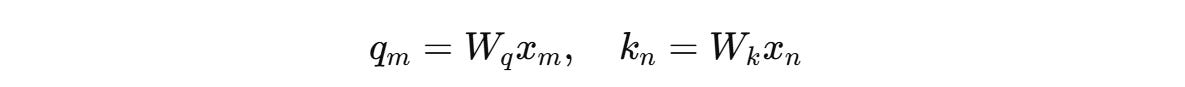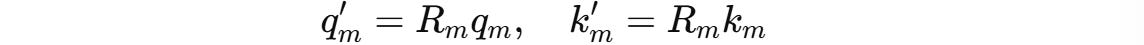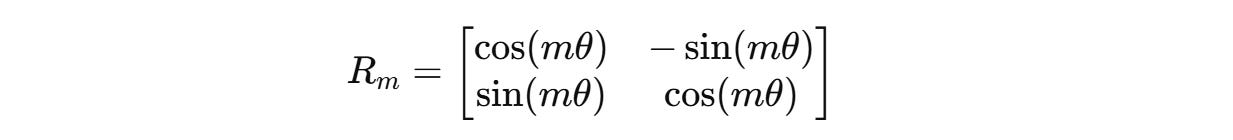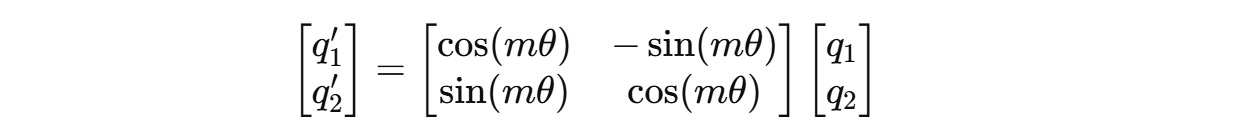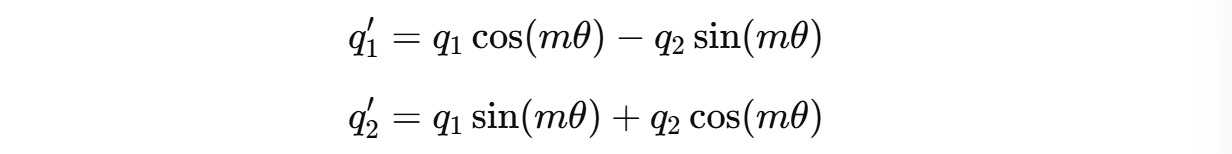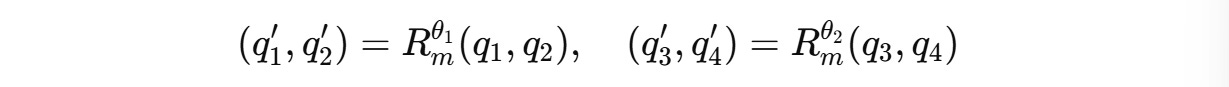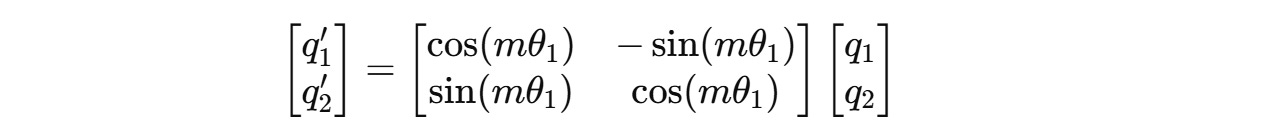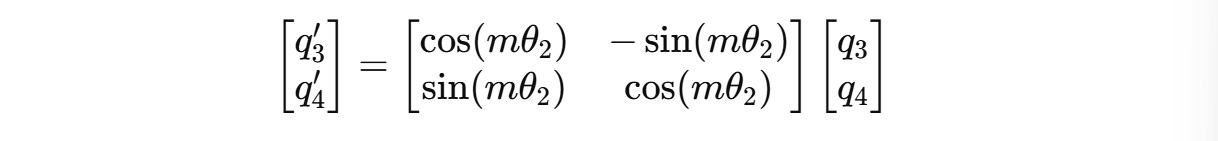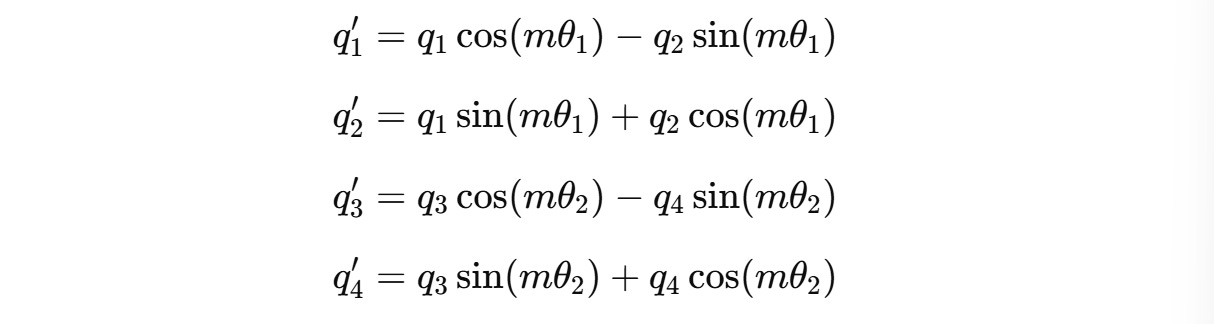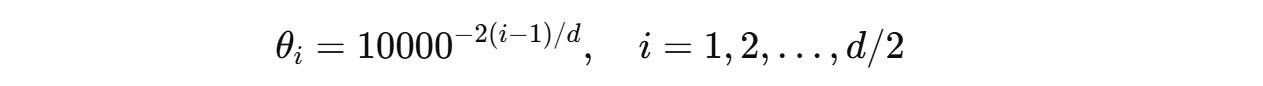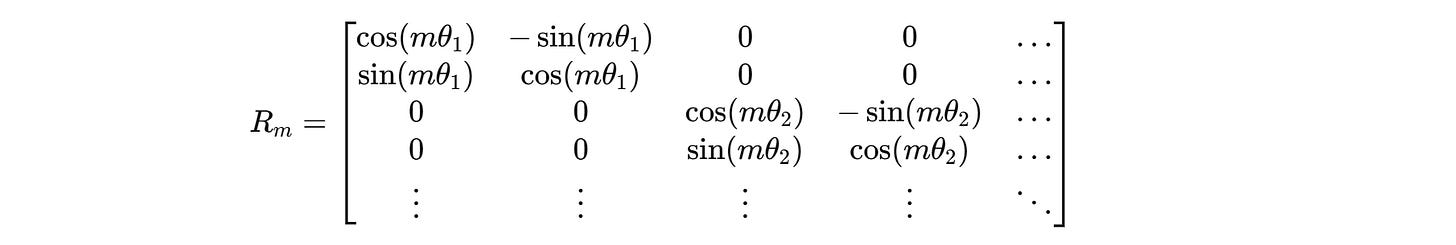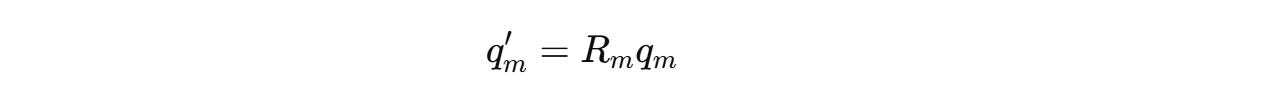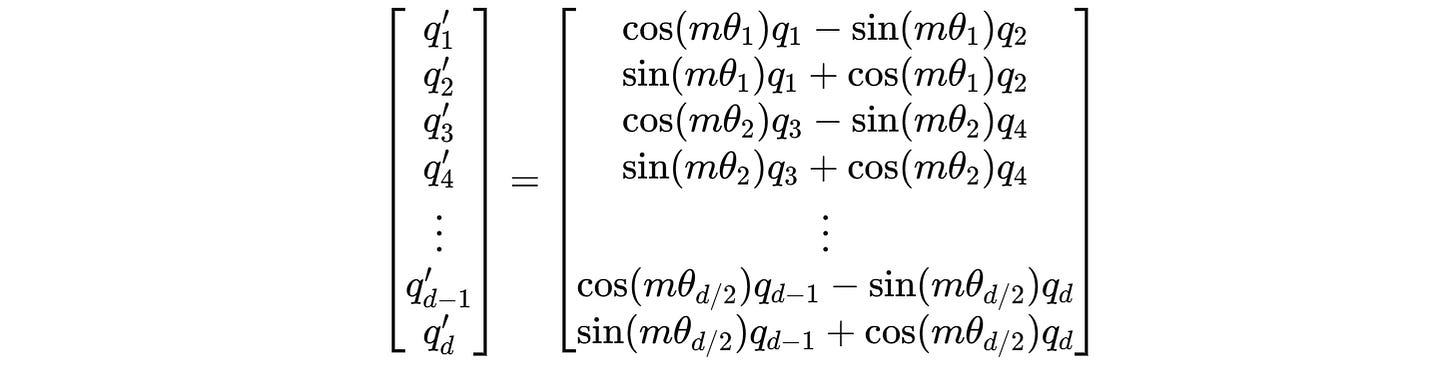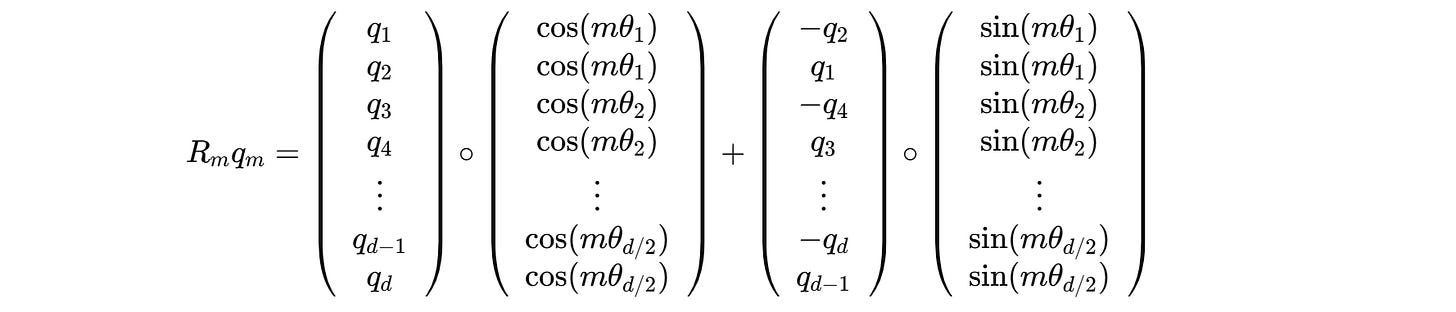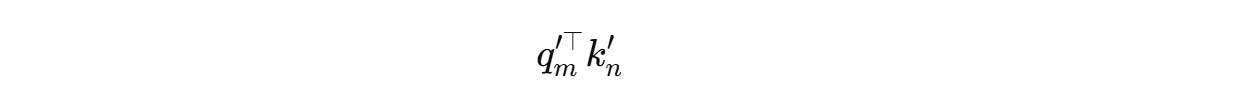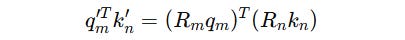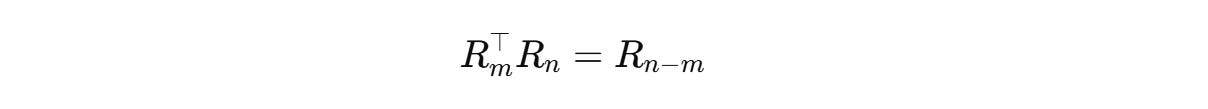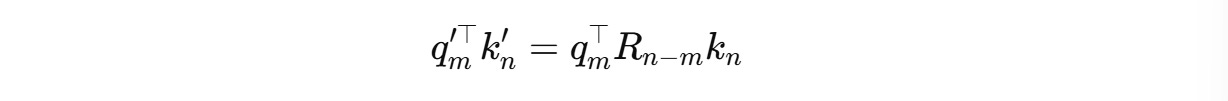Revisiting The Basics: Rotary Position Embeddings (RoPE)

A lesson on Positional Embeddings from the ground up.

Feb 08, 2025

Transformers process tokens in parallel rather than sequentially.

This is what gives them the computational advantage over RNNs.

However, this also makes Transformers position-agnostic, meaning they do not have a sense of the order of the tokens they process.

Consider these two sentences:

“The cat sits on the mat.”
“The mat sites on the cat.”

To a Transfromer, both of them are the same.

This isn’t good for language processing.

Therefore, positional information in the form of positional embeddings (vectors) is added with token embeddings before Transformers process them.

The Transfromer architecture where the addition of Positional Encoding to the Input embedding can be seen in the lower left and right corners (Image obtained from the research paper titled ‘Attention Is All You Need’ )

Types Of Positional Embeddings

Positional Embeddings are of two main types:

Absolute Positional Embeddings — where each token is assigned a unique encoding according to its position
Relative Positional Embeddings — where information about how far apart tokens are from each other is encoded rather than their absolute positions

Each of them can be either:

Fixed (calculated using a mathematical function)
Learned (has trainable parameters that are updated with backpropagation during model training)

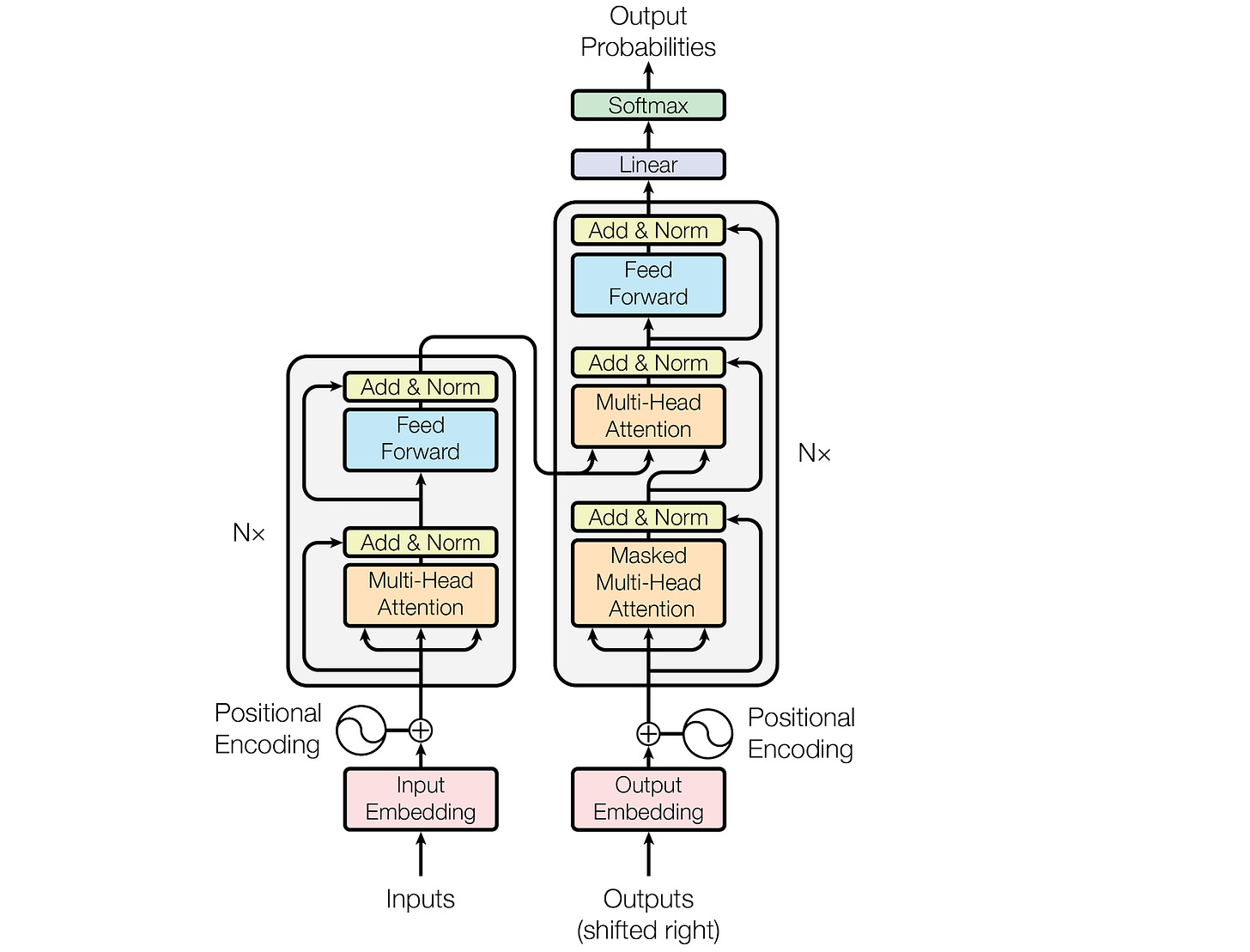
Positional Embeddings In The Original Transformer Paper

While relative positional embeddings are popularly used by the T5 Transformer, in the original Transformers paper, the authors use fixed absolute positional embeddings, as shown below.

(Learned positional embeddings are not used in this paper because the fixed embeddings produced nearly identical results.)

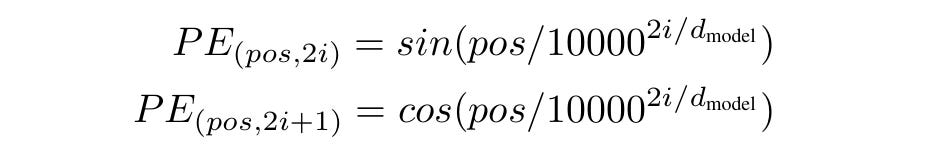
Calculations for Positional Embeddings where ‘pos’ is the token index, ‘i’ is the index of the token embedding dimension, and ‘d’ is the total token embedding dimension

For each token position, Positional embeddings (PE) are calculated using alternating sine and cosine functions on even and odd dimensions, respectively.

The denominator 10000 ^ (2i/ d(model)) controls the wavelength of these functions.

This means that for lower dimensions (smaller i), the frequency is high, and the wavelengths are short.

Similarly, for the higher dimensions (larger i), the frequency is low, and the wavelengths are long.

These wavelengths form a Geometric progression, with the smallest and the largest values being 2π and 10000 × 2π , respectively.

This makes the model capture the short-term and long-term dependencies in the input sequence using the high and low frequencies, respectively.

Since the dimensions of these positional embeddings are the same as those of the token embeddings, they can be directly summed as follows before being passed to the Transformer for processing.

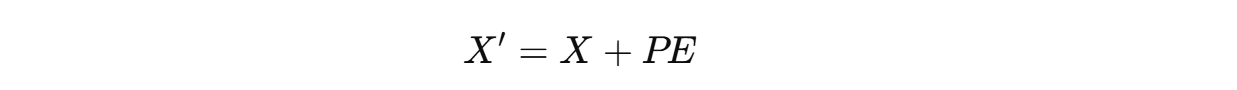
X’ is the final input embedding passed into the Transformer, X is the original input embedding, and PE is the set of positional embeddings for each token in the input sequence.

These embeddings can also capture the relative relationships between tokens, as their positional embeddings are related linearly (but are not the best for this).

Improving Learning Further With RoPE

Previous embedding approaches can struggle to capture dependencies in sequences longer than those seen during training.

These approaches also add positional embeddings to the token embeddings, which increases the total parameters and complexity. This leads to increased computational training costs and slower inference.

A 2023 research introduced a new way of directly encoding both absolute and relative positions in the attention mechanism.

Their method is called Rotary Position Embedding or RoPE.

Instead of adding position embeddings, as in the previous approaches, RoPE rotates the token embeddings according to their positions.

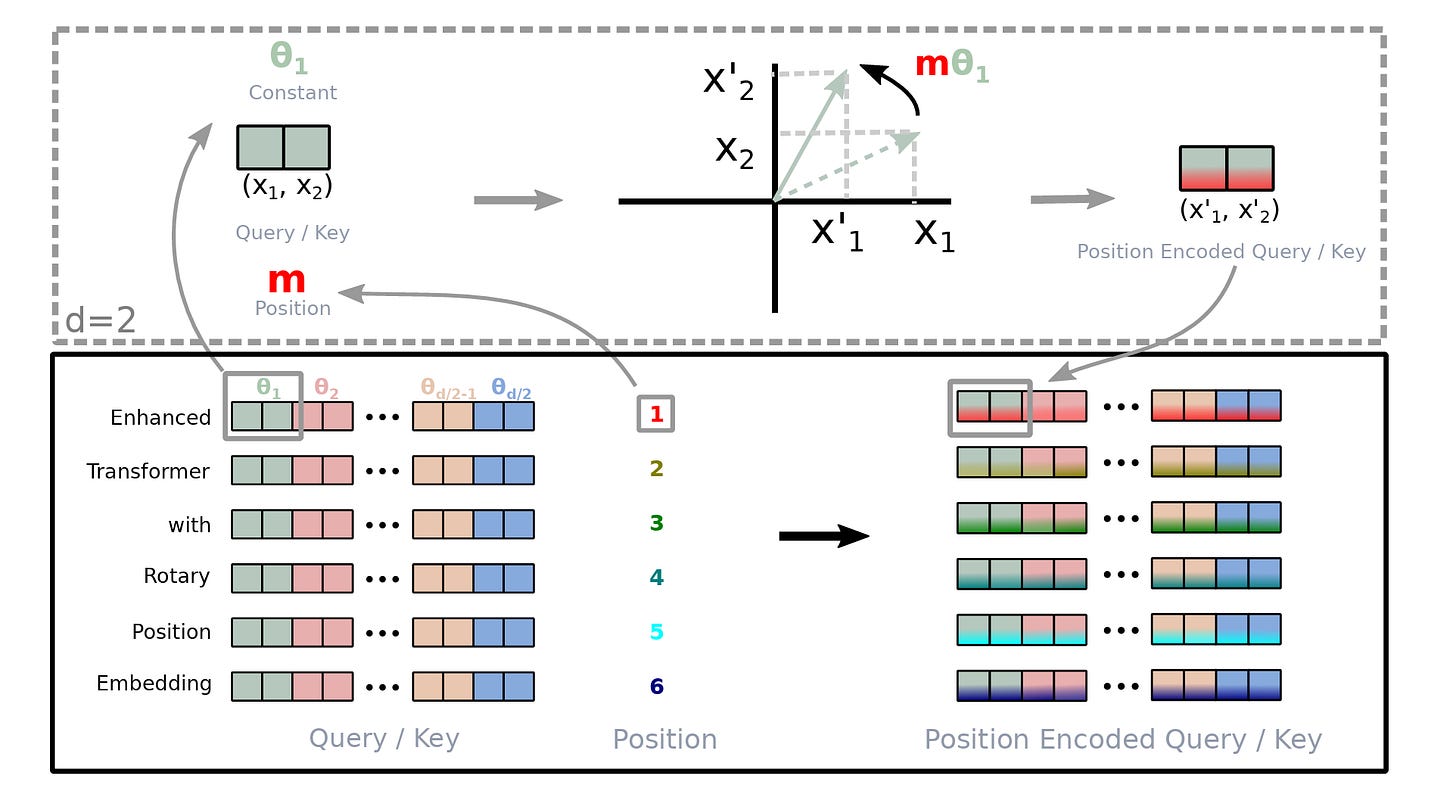
For a token embedding x(m) of dimension d at position m, it is transformed into Query (q(m)) and Key (k(n)) vectors as follows using weight matrices W(q) and W(k), respectively.

RoPE rotates these vectors before they are used in the attention calculation. This is done using a position-dependent rotation matrix R(m).

R(m) acts independently on each pair of dimensions in q and k.

For a case where these vectors are two-dimensional (d = 2), the rotation matrix R(m) is defined as:

This 2D rotation matrix rotates these vectors counter-clockwise, proportional to their position m by an angle of mθ where θ is a constant (1 in the case of d = 2).

For a two-dimension query vector q(m) = (q1, q2) , this transformation will result in:

However, query and key vectors are usually higher-dimensional (assumed an even number of dimensions).

To work with them, they are paired, and separate 2D rotations are applied to each adjacent pair of dimensions.

For example, for a 4-dimension query vector q(m) = (q1, q2, q3, q4), two independent rotations are applied for (q1, q2) and (q3, q4) as shown below.

These can be expanded to:

The angle of rotation θ(i) for each pair of dimensions is different and is calculated as follows:

This ensures that the low-frequency rotations for higher dimensions capture long-range dependencies and the high-frequency rotations for lower dimensions capture short-term dependencies.

This θ is similar to what we learned when describing the sinusoidal embeddings from the original Transformers paper.

The overall rotation matrix for higher dimensions looks as follows.

Making Calculations Computationally Efficient

One can avoid explicit matrix multiplication to make the process of computing the rotated queries and keys computationally efficient.

This can be done by precomputing cos⁡(mθ(i)) and sin(mθ(i)) for each position m, and then performing simple element-wise multiplications and additions between the terms.

For example, this is how we calculated the rotated query q’(m) previously:

This can be changed to:

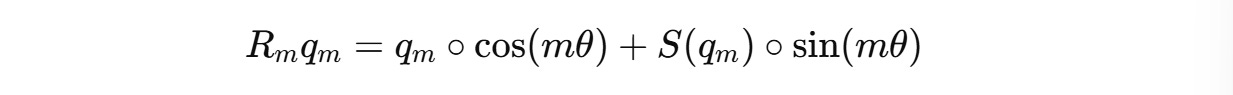
The computationally efficient calculation for R(m)q(m) where ∘ represents element-wise multiplication and S(q(m)) operation swaps adjacent elements in q(m), negating the even-indexed ones

The complete calculation is shown below:

This reduces the time complexity from O(d^2) to O(d) by avoiding explicit matrix multiplication.

Calculating Attention Score

Next, the attention score is calculated as the dot product between the rotated queries and keys as follows:

This can be expanded to:

Since the rotation matrices can be written as follows,

The equation becomes:

Thanks to RoPE, the attention score now encodes the relative position of tokens (n − m) without needing additional relative embeddings.

Visual representation of RoPE embeddings (Image from the ArXiv research paper titled ‘RoFormer: Enhanced Transformer with Rotary Position Embedding’)

RoPE Decay For Long Inter-Token Dependencies

There’s another cool property of these embeddings: the relative importance of the connection between far-apart tokens is lower than closer ones.

The RoPE research paper provides a mathematical explanation for this, and curious readers are encouraged to read it.

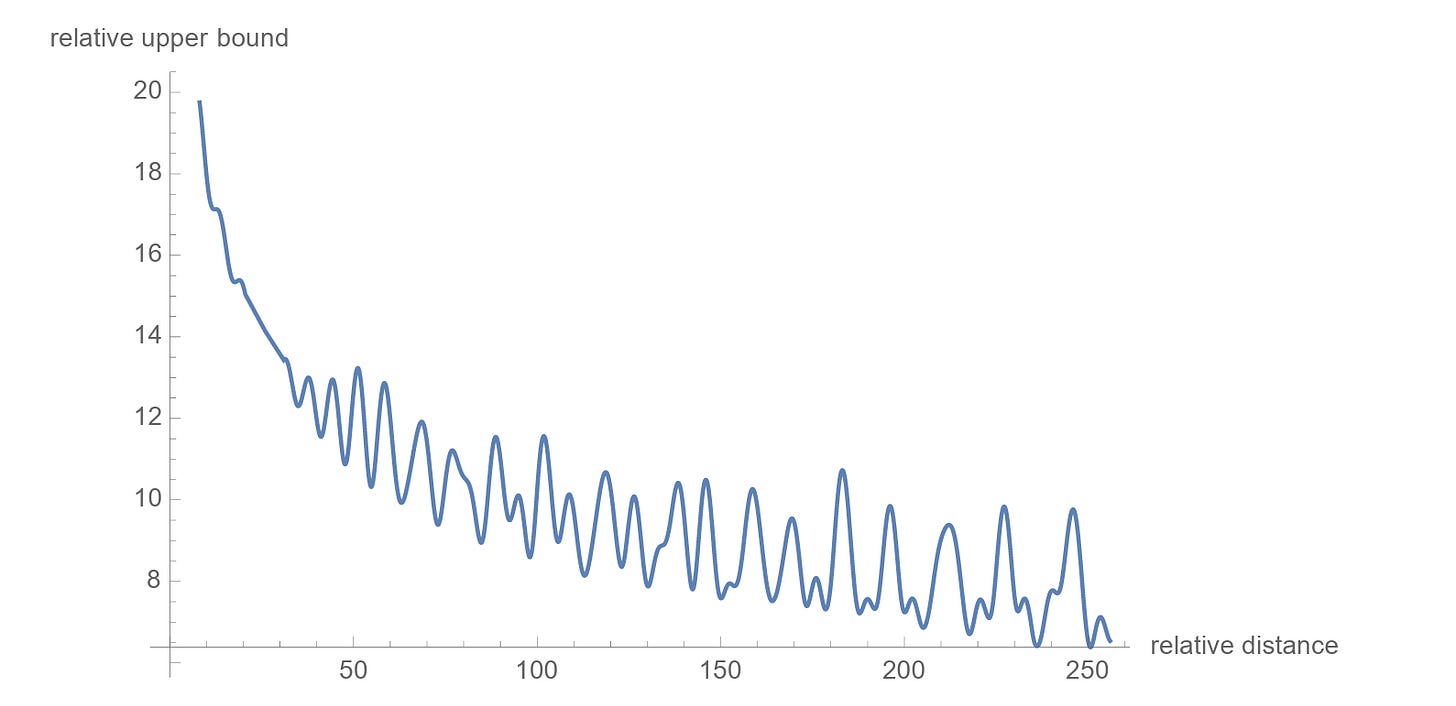
Graph showing the decay of attention scores in RoPE as the relative distance between tokens increases. The further two tokens are apart, the weaker their maximum possible attention score becomes. (Image from the ArXiv research paper titled ‘RoFormer: Enhanced Transformer with Rotary Position Embedding’)

(Although the original research paper supports this notion, some new research has shown that this might not always be true, and the decay in long-term dependencies is not a universal property of RoPE.)

Which LLMs Use RoPE Today?

RoPE is one reason for the phenomenal performance achieved by modern-day LLMs, such as Meta’s Llama 3 models and Google’s Gemma models.

DeepSeek-V3 also uses a modified version of RoPE that is compatible with its modified version of Multi-head Attention called Multi-head Latent Attention.