We Have Finally Found A Solution To An Extremely Energy Efficient AI
A deep dive into the 'L-Mul' or Linear complexity multiplication algorithm that makes our existing AI models faster and more energy-efficient than ever before.
Running AI models is expensive and costs the environment.
The average electricity consumption of running ChatGPT in early 2023 was 564 MWh each day.
This is equivalent to the total daily electricity usage of 18,000 families in the United States.
It is also estimated that, in the worst-case scenario, Google’s AI service could consume as much electricity as Ireland's.
This is quite a lot! But why does AI need so much energy?
Neural network internals work with floating point parameters, which involve high-dimensional tension multiplications, element-wise multiplications, and linear transformations.
And these operations are energy-expensive.
If we could tweak the amount of computation needed with these operations in these neural networks, we could save a lot of energy and speed them up.
Amazingly, researchers of a recent pre-print published in ArXiv have proposed to solve exactly this.
They created an algorithm called ‘L-Mul’, or the linear complexity multiplication algorithm, which can approximate floating point multiplications with integer addition operations.
This algorithm can be integrated into existing neural networks without any need for fine-tuning.
This change phenomenally leads to a 95% reduction in energy consumption for element-wise floating point tensor multiplications and up to 80% energy savings for dot product computations.
Here’s a story in which we deep-dive into this algorithm and discuss how it makes our existing AI models faster and more energy-efficient than ever before.
Let’s go!
Let’s First Talk Numbers
Neural networks use floating point tensors to represent their inputs, outputs and parameters.
The 32-bit (default for PyTorch) and 16-bit FP tensors (FP32 and FP16) are commonly used for this purpose.
The IEEE 754 standard defines the technical standards for arithmetic on these floating point tensors.
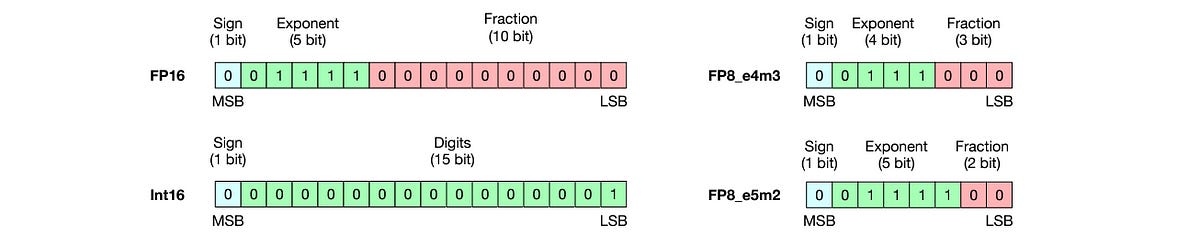
Next, let’s discuss operations.
The computational complexity of integer addition is linear, i.e. O(n), where n is the number of bits.
But floating point multiplication requires exponent addition (O(e)), mantissa multiplication (O(m²)) and rounding, where e and m represents the number of bits for the exponent and mantissa.
There’s an energy cost to this.
Floating point operations are more expensive than integer operations.
Multiplying floating point numbers is more costly than adding them.
Specifically, multiplying two 32-bit floating-point numbers (FP32) consumes 4 times the energy of adding two FP32 numbers and 37 times more energy than adding two 32-bit integers (Int32).

How can we replace these floating-point calculations with less expensive integer operations?
Here Comes The ‘L-Mul’ Algorithm
L-Mul stands for Linear-Complexity Multiplication.
The main idea behind this newly developed algorithm is to approximate the costly floating point multiplication with simpler, linear-complexity integer addition while maintaining similar precision.
Let’s first understand what a traditional floating-point multiplication involves.
Two floating point numbers x and y, can be represented as:
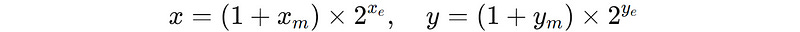
The result of multiplying these numbers is as follows:
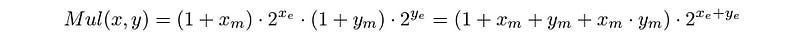
The overall process involves Mantissa multiplication and Exponent addition.
On Matissa multiplication, if the result exceeds 2, it is normalized, and the carry is moved to the exponent.
After normalization, if needed, the mantissa is rounded to fit to the bit width.
In the final step, the XOR operation is used to decide the sign of the result.
Notably, the Mantissa multiplication is the most computationally expensive part of this process.
The time complexity of this step is O(m²), where m is the number of bits in the mantissa.
The L-Mul algorithm replaces this step with Integer addition.
Here, the multiplication of mantissa is replaced by a series of integer additions, making the time complexity linear, i.e. O(n) where n is the bit size of the floating point number.
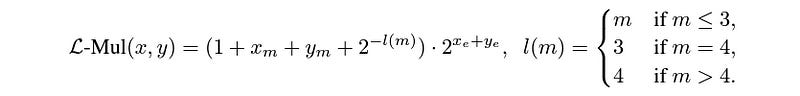
The term l(m) is the offset exponent and is used to adjust for the reduced precision caused by removing full multiplication, and its size depends on the size of the mantissa as follows:
l(m) = mfor mantissa less than or equal to 3 bits.l(m) = 3for mantissa equal to 4 bits.l(m) = 4for mantissa larger than 4 bits.
When the sum of mantissa x(m) and y(m) exceeds 2, a carry is directly added to the exponent, skipping the need for normalization and rounding as in traditional floating point multiplication.
Finally, similar to traditional multiplication, the sign of the final result is calculated by XOR-ing the signs of the input numbers.
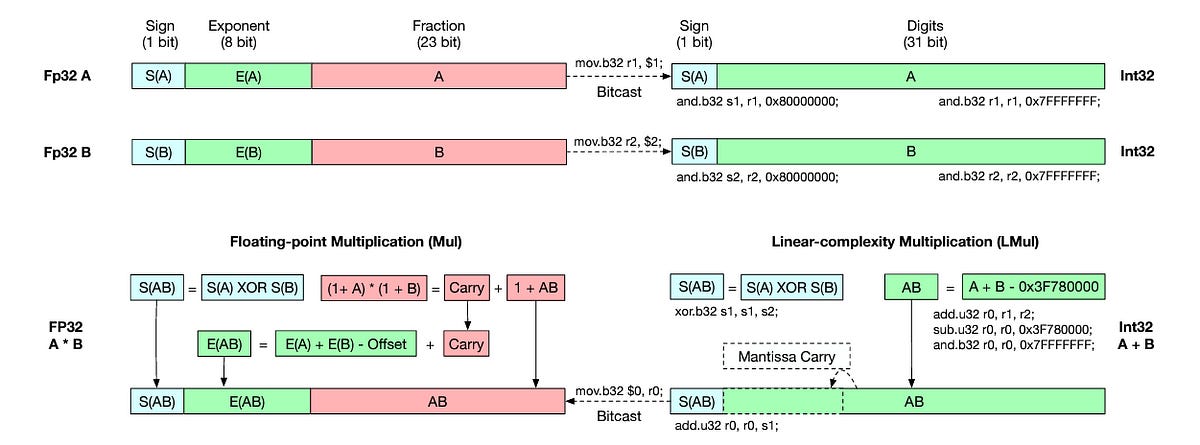
$1 and $2 are the registers storing FP32 inputs, $0 is the register storing the FP32 output and s1, s2, and r0 store intermediate Integer results. (Image from the original research paper)How does this apply to LLMs, as you’d ask?
The L-Mul algorithm can be directly applied to the attention mechanism of a transformer (without any model fine-tuning) as follows:
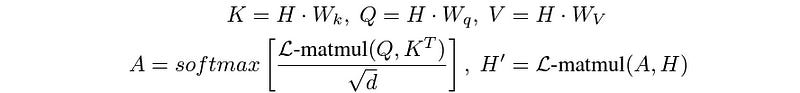
What’s So Good With ‘L-Mul’?
Precision & Computational Cost
8-bit floating point numbers (FP8) are gaining popularity these days.
This is because they reduce the computational cost and memory use while maintaining the required accuracy for training and inference of ML models.
FP8_e4m3 and FP8_e5m2 are the common choices for these 8-bit representations. (Here, e and m represent the number of bits used for the exponent and mantissa.)
FP8_e4m3 offers more precision (due to larger mantissa) but has a limited range of values it can represent (due to a smaller exponent).
On the other hand, FP8_e5m2 offers more range but less precision.
FP8_e5m2 is also more computationally efficient because of the smaller mantissa.
But when compared, L-Mul is found to be more precise than FP8_e4m3 multiplications, and it uses fewer computation resources than FP8_e5m2, making it a highly efficient alternative to both.
Gate Complexity
Regarding the number of gate-level computations needed by digital circuits to perform L-Mul and FP8 multiplications, L-Mul is found to be both more efficient and more accurate than FP8 multiplication.
Evaluation On Real-World Tasks
L-mul can replace tensor multiplications in attention mechanisms without losing performance.
This reduces the energy cost of attention calculations by 80%.
On the other hand, although FP8 multiplication can reduce energy costs due to its lower precision, it reduces accuracy during model inference.
On text-based tasks, using L-mul in Mistral-7b-Instruction-v0.3 and Llama-3.1–8B-Instruct and testing on multiple benchmarks, L-Mul performs significantly better than FP8 in most experiments.
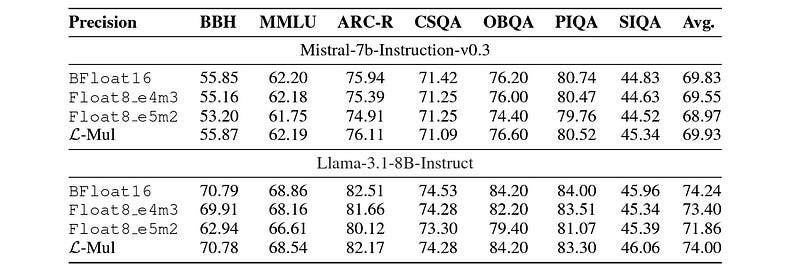
Similar performance improvements are seen in GSM8k (Grade School Math Problems).

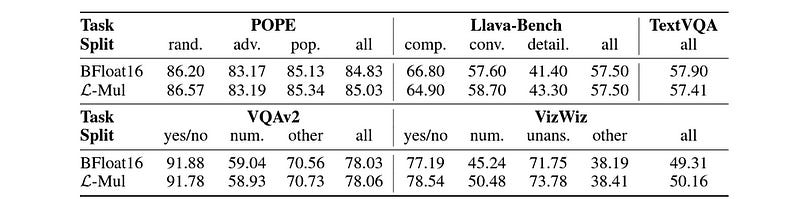
When tested with the Llava-v1.5–7b model on:
Visual question answering (VQA) using VQAv2, VizWiz, and TextVQA datasets
Object hallucination using the POPE dataset, and
Instruction-following tasks using Llava-Bench
L-mul again has better performance than FP8 and Bfloat16, on most tasks.
You must be wondering what happens when a model is fine-tuned with L-mul used in its parameters?
When all multiplication operations in the Gemma2–2b-It model are replaced with FP8_e4m3 L-Mul, and compared with a standard fine-tuned FP8_e4m3 model, it is seen that both have similar performances.
This is an important finding because it means that L-mul can even make a fine-tuned LLM energy efficient without compromising its accuracy!
Imagine how efficient our AI models will be when algorithms like L-mul are implemented in them!
I am excited about the future.
What are your thoughts on it? Let me know in the comments below.


