XNets Are Here To Beat MLPs & KANs (& How Can You Train One From Scratch)

A deep dive into XNet, a novel neural network architecture that beats the performs of MLPs and KANs in recent experiments

Generated with DALL-E 3

A recent research publication in ArXiv described a novel neural network architecture called XNet or CompleXNet.

This architecture uses a new activation function called the Cauchy Activation Function, which is derived from the Cauchy Integral Theorem in complex analysis.

Surprisingly, XNets are highly effective for image classification tasks and significantly outperform MLPs on established benchmarks like MNIST and CIFAR-10.

They have superior performance, particularly in handling complex high-dimensional functions, compared to KANs.

They also have substantial advantages over Physics-Informed Neural Networks (PINNs) for solving low- and high-dimensional partial differential equations (PDEs).

---

But First, What Is The Cauchy Activation Function?

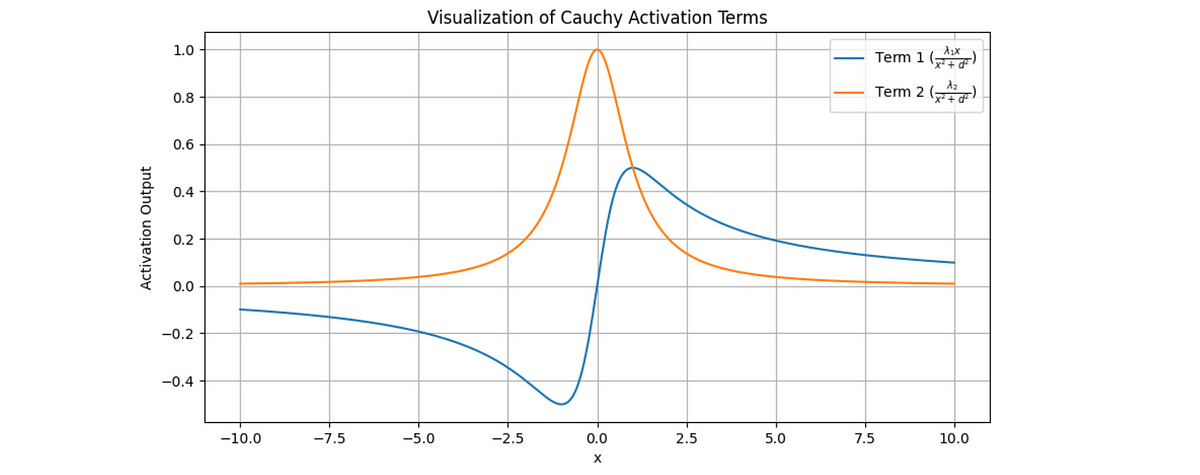
The Cauchy activation function is derived by modifying Cauchy kernels to fit a form suitable for neural network nodes.

It looks like the following:

Cauchy activation function where λ1, λ2, and d are trainable parameters

The function can approximate any smooth function to its highest possible order (as proven mathematically).

There is something else special about it.

The function is localized and decays at both ends. 

This decay property means that the function’s output diminishes as the input moves farther from the centre, allowing it to focus more on nearby data points rather than the ones farther away.

Visualisation of the two terms of the Cauchy activation function

Changing the activation function of traditional MLPs to the Cauchy activation function is the main modification in XNets.

Alongside this, the architecture of the resulting networks (like layer depth or node count) can be simplified without losing performance or accuracy.

---

Building An XNet From Scratch

To build an XNet, we will first code the Cauchy Activation function. 

I am using PyTorch for this example.