R-Zero: A Method For Training Reasoning LLMs With Zero Data Is Here
A deep dive into the R-Zero framework that helps LLMs self-evolve to get better at reasoning without using any external training data.
We need Self-evolving LLMs (that can learn and improve from their mistakes) to reach Artificial Superintelligence.
However, our current methods for improving LLMs rely on training them with large amounts of human-curated data.
Sure, we are getting some impressive results with this approach, but we will soon hit a dead end once we run out of human-generated data to train LLMs on.
There’s also another issue that human-curated data won’t let LLMs progress beyond the capabilities of human intelligence. We will need some other approach to achieve this.
What if there were a way for an LLM to identify its weaknesses, generate its own training data, and improve itself based on this data, all autonomously?
Surprisingly enough, a group of researchers has now made this possible.
In their recent research preprint published in ArXiv, they introduced R-Zero, which is an entirely autonomous framework that enables an LLM to generate its own training data from scratch and helps it to learn and improve using it.
Results show that R-Zero is highly effective in improving the reasoning capability of LLMs on multiple math and general-domain reasoning benchmarks.
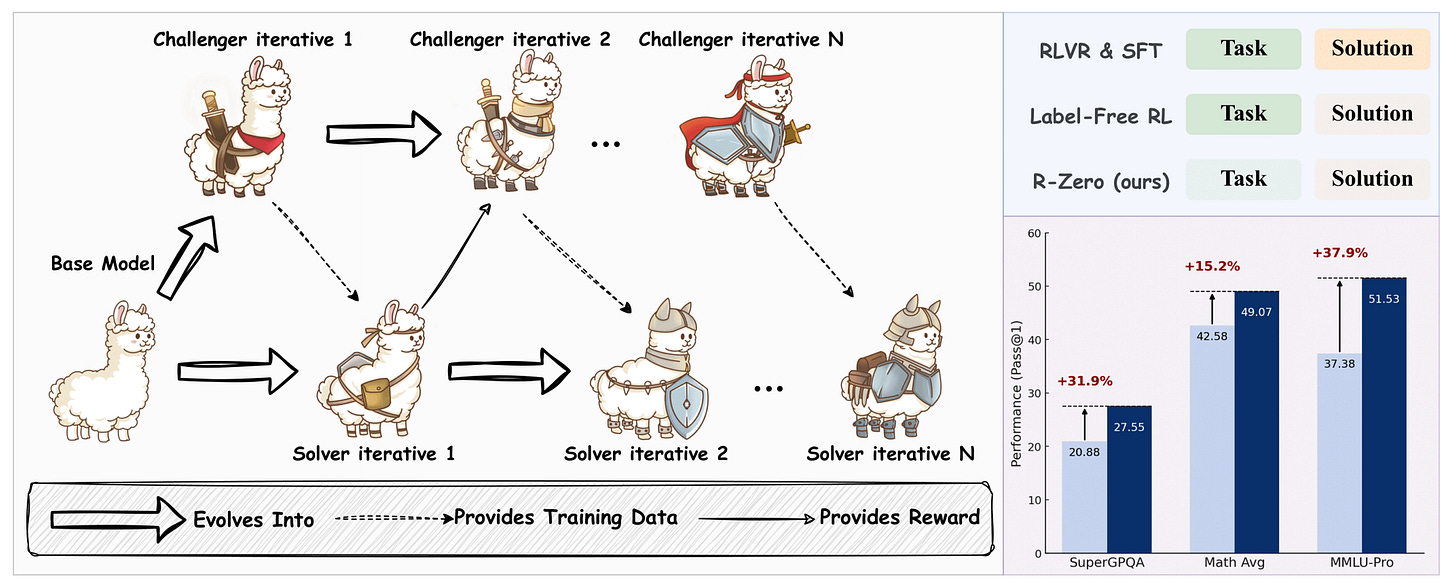
Here is a story where we deep dive to learn how R-Zero works, and discover if we have finally found a way towards Self-evolving LLMs.
Let’s begin!
My latest book, called “LLMs In 100 Images”, is now out!
It is a collection of 100 easy-to-follow visuals that describe the most important concepts you need to master LLMs today.
Grab your copy today at a special early bird discount using this link.
But First, What Are Self-Evolving LLMs?
Self-evolving LLMs are a category of LLMs that can autonomously spot their weaknesses and learn from their own experiences to improve themselves.
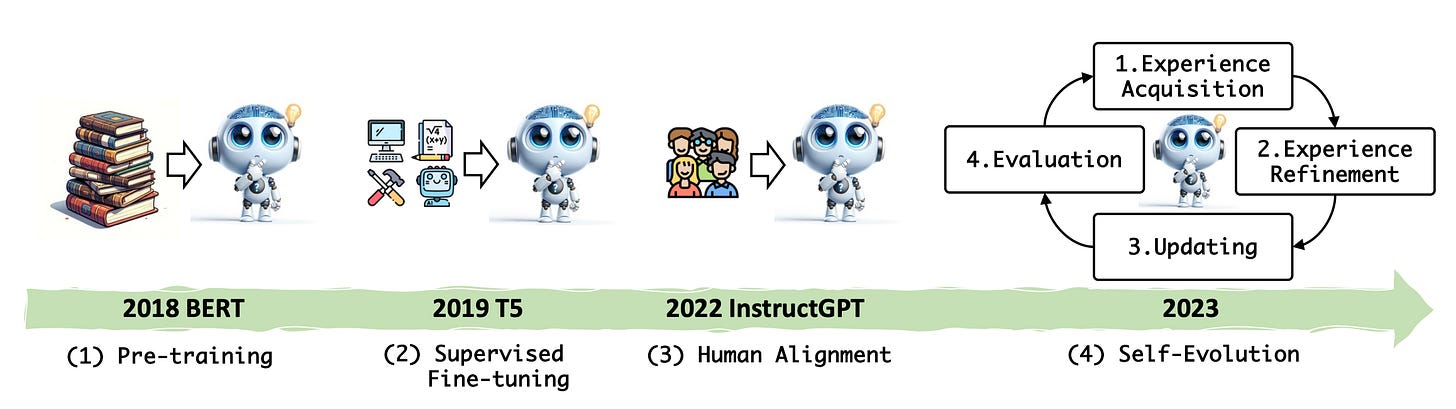
Many of the current self-evolving LLMs rely on human expert-curated datasets consisting of tasks/questions and their ground truth answers/ labels.
Labels from these datasets give an improvement signal to LLMs during training using Supervised Fine-Tuning (SFT) or Reinforcement Learning with Verifiable Rewards (RLVR).
If you’re new to RLVR, it is a technique for fine-tuning LLMs that uses a rule-based verifier (that gives a binary reward as 1 if the output passes the correctness check, and 0 otherwise) to guide the training process.

Human-curated data isn’t easy to assemble. Creating such datasets requires domain experts, which makes it very expensive, highly time and labour-intensive, and therefore difficult to scale.
Such data also puts a bottleneck on LLMs and makes it difficult to train them to reach super-human capabilities.
To reduce dependence on these datasets, many methods have been developed that can train LLMs without requiring a reward signal from human-annotated labels.
Such methods are called Label-Free Reinforcement Learning methods, where improvement (reward) signals can be directly obtained from the model’s own outputs instead of from external labels.
Some examples include:
Reward based on Sequence-level confidence: Reward the answers that the model is most confident about.
Reward based on Self-Consistency across reasoning paths: Reward answers that stay consistent through multiple reasoning routes.
Reward low output entropy: Reward more certain/ less random answers.
Random reward: Assign rewards at random to encourage exploration.
Negative reward: Penalize incorrect answers.
Although these methods do not require external labels as a reward signal and can use internal rewards for this purpose, they still need datasets of unlabelled problems for LLM training.
This too has been addressed in previous research, which describes how LLMs can train on problems generated by themselves (Self-challenging LLMs).
This approach works well in domains like mathematical problem solving and code generation, where self-generated tasks and solutions can be checked for correctness using a code executor/ verifier.
However, verifiers like these are not available for problems involving open-ended reasoning, which makes it hard to apply these methods in such cases.
R-Zero works around this limitation and checks for task quality and correctness using intrinsic signals from the LLM itself.
Let’s discuss how it makes this possible in depth next.
Here Comes ‘R-Zero’
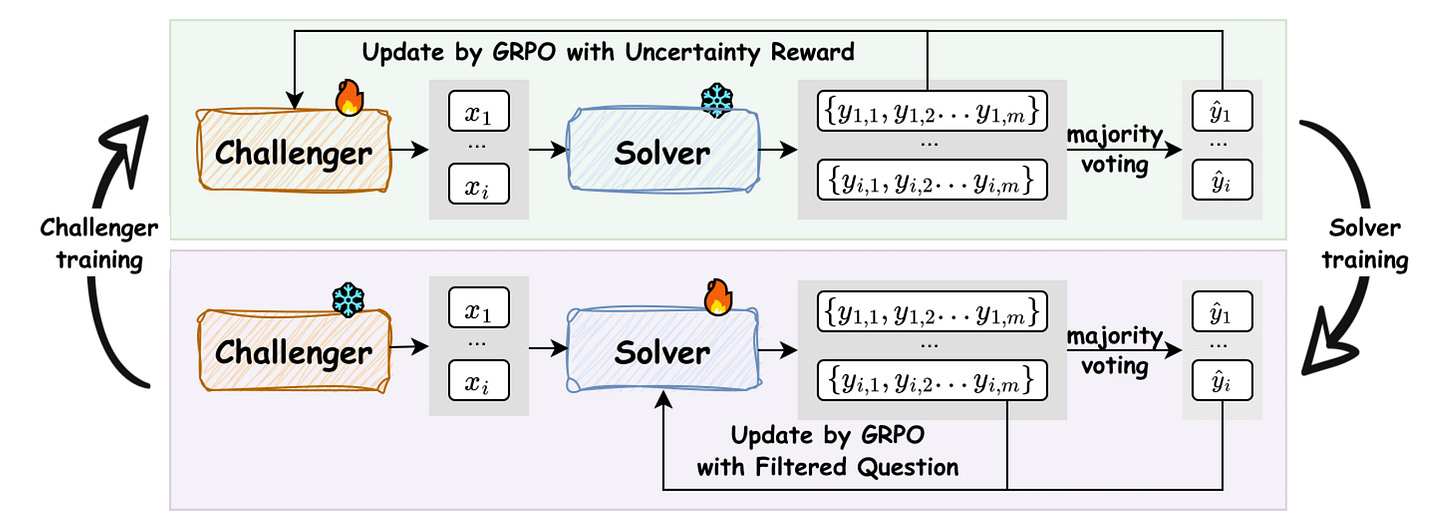
R-Zero borrows from an approach called Self-play, where a single LLM takes on two different roles that challenge each other, working iteratively, leading to mutual improvement.
In the case of R-Zero, the two roles/ versions coming from a single base LLM are:
Challenger: which generates challenging problems at the edge of the Solver’s problem-solving capability.
Solver: which tries to solve the problems the Challenger produces.
Both of these versions operate and improve in an iterative loop, where the Challenger learns to create increasingly difficult tasks, and the Solver learns to solve them.
The entire process is self-supervised and requires no human intervention at any step.
Let’s now discuss the workings of different components of R-Zero in more detail.
Training The Challenger
The purpose of Challenger (represented by Q(θ)) is to generate challenging mathematical questions. These questions are aimed to be solvable, but at the edge of the Solver’s problem-solving capabilities, neither too easy nor too hard.
An Uncertainty reward is used to guide the Challenger to generate such questions.
For each generated question x, the Solver (represented by S(Φ)) answers it m times.
The Solver’s responses are represented by the set {y(1), …, y(m)}.
The most common answer from this set acts as the pseudo-label (ỹ(x)) for the question x.
It is then checked what fraction of the Solver’s answers match this pseudo-label. This is the Solver’s empirical accuracy, represented by p̂.
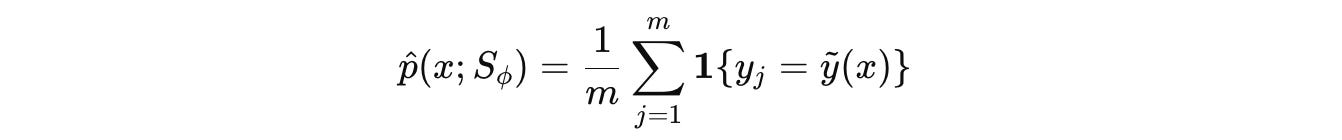
ỹ(x) is the pseudo-label, 1{⋅} represents an indicator function that returns 1 if the condition is true and 0 otherwiseFinally, the Uncertainty reward is calculated as:
This reward peaks when p̂ = 0.5 which means that it peaks when the Solver solves a question correctly in half of its attempts.
This represents the point of maximum uncertainty for the Solver, and this is the level of questions that we want the Challenger to generate.
The Challenger might try to hack this reward by repeatedly generating the same or similar questions. To discourage this, a Repetition penalty (a type of negative reward) is used.
For two questions x(i) and x(j), their BLEU similarity score is calculated where 1 means identical, 0 means completely different questions.
Subtracting this score from 1 converts it into a distance (d(i)(j)), where:
If the two questions are identical (BLEU score of
1), their distance will be0.If the two questions are completely dissimilar (BLEU score of
0), their distance will be1.
Questions whose distance is below a certain threshold τ(BLEU) are considered similar and are grouped into clusters represented by the set C = {C(1),... , C(k)}.
The penalty score for a question x(i) in a cluster C(k) is proportional to the size of its cluster:
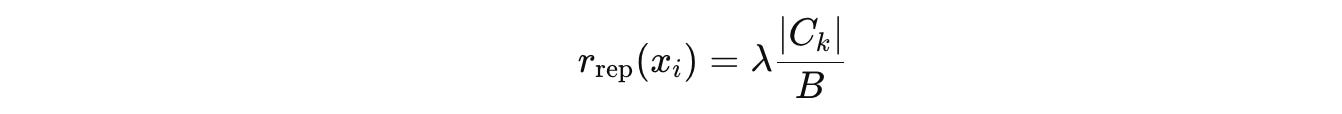
This means that the larger a cluster is, the more similar questions it has, and the bigger penalty these questions get. This pushes the Challenger towards generating more diverse questions.
Before calculating the total final reward for the Challenger, it is first checked whether the Challenger’s generated output correctly encloses the questions within <question> and </question> tags or not.
If an output fails this check, it is immediately given a reward of 0 and no further rewards are computed for it. Consider this as an Incorrect Format penalty.
For outputs that pass this format check, the final composite reward is calculated as follows:
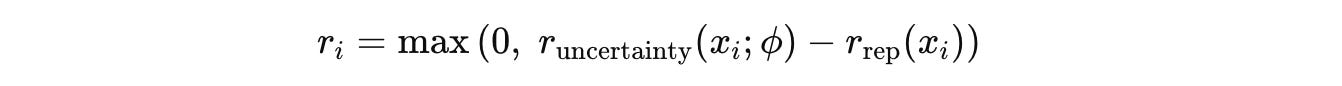
For a batch of G questions and their rewards {r(1), …, r(G)}, the Advantage Â(i) for each question is computed.
The Advantage is a normalized score that measures how much better or worse a Challenger-generated question’s composite reward is compared to other questions in the same batch.
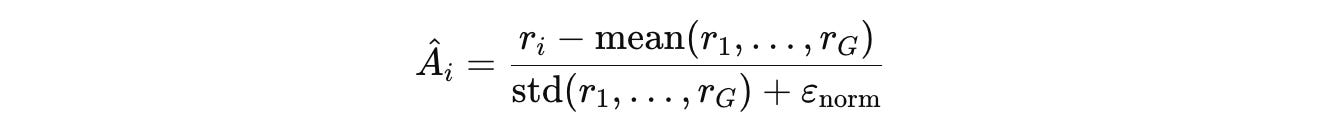
This value is then used to update the Challenger policy (parameters in case of an LLM) Q(θ) by minimizing the GRPO loss to generate more high-advantage questions.
The following equation shows that the GRPO loss, where the clipping and KL penalty keep the policy from drifting too far in one update.

Creating A Training Dataset For The Solver
Once the Challenger is updated as discussed above, it is used to generate a large pool of N questions.
For each question x(i), the Solver answers it m times, and the most frequent answer becomes the pseudo-label ỹ(i) for the question.
A question-answer pair (x(i), ỹ(i)) is added to the Solver’s training set S only if:
where p̂ is the Solver’s empirical accuracy for the i-th question.
This condition keeps only those questions where the Solver’s accuracy is close to 50%, within a margin of δ. Simply put, it filters and discards the questions that are too easy or too difficult.
Training The Solver
Once the training dataset S is created, as discussed in the step above, the Solver, represented by S(Φ), is fine-tuned on it.
The reward for this step is quite straightforward.
For each question x(i) in the dataset with pseudo-label ỹ(i), the Solver generates multiple answers x(j) for it.
Each answer gets a simple binary reward r(j):
Next, the binary rewards are normalized to get an advantage Â(j) for each answer.
These values are then used to update the Solver’s policy by minimizing the GRPO loss, making it more likely to produce the correct answer (matching the pseudo-label) to hard questions that the Challenger generates in the future.
The complete process of how R-Zero works is shown in the illustration below.
How Well Does R-Zero Perform?
R-Zero is tested on two different families of LLMs:
Qwen (Qwen3–4B-Base and Qwen3–8B-Base models)
OctoThinker (OctoThinker-3B and OctoThinker-8B models derived from continually training Llama 3.1)
The resulting models are then tested on multiple mathematical and general domain reasoning benchmarks.
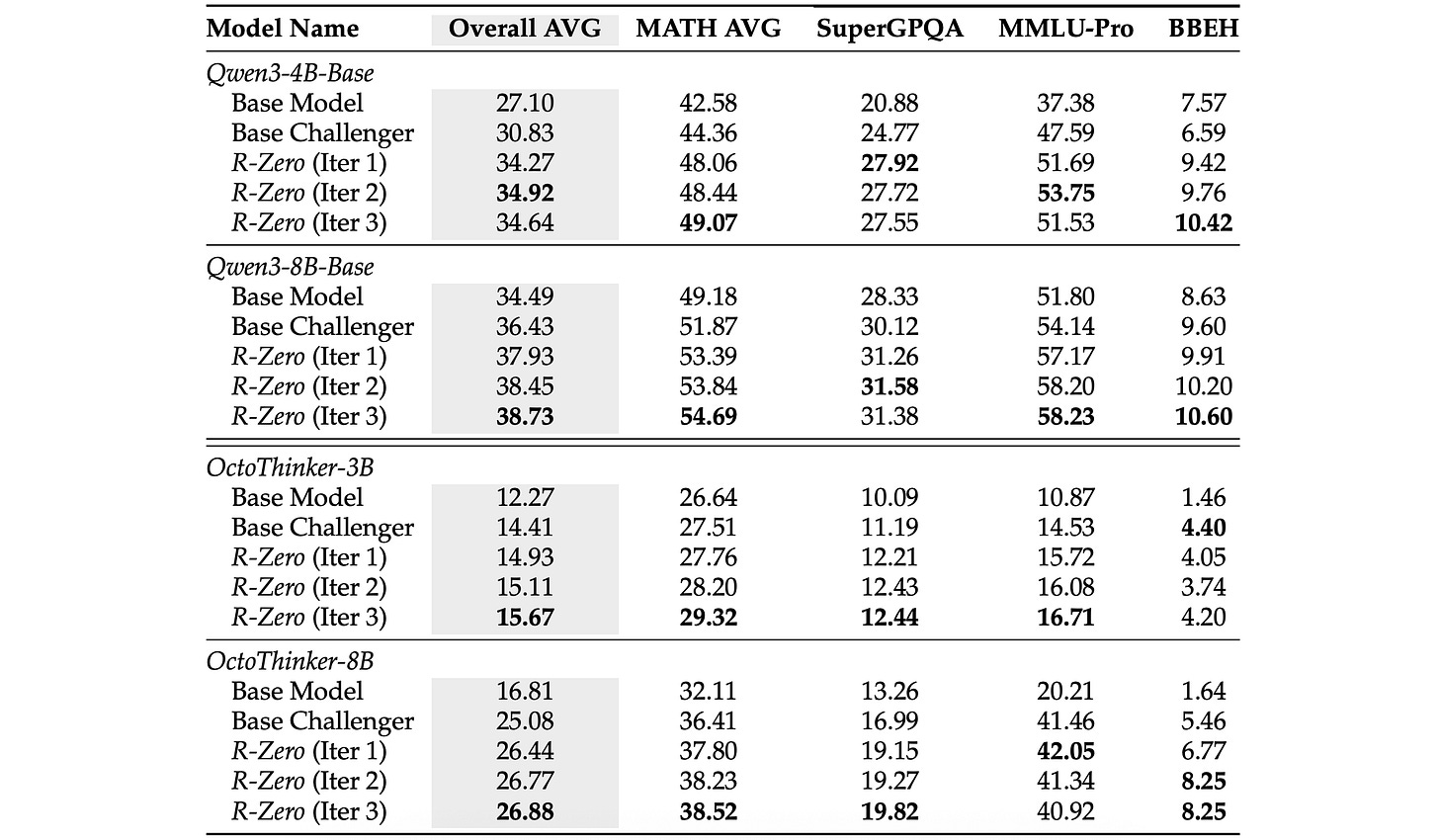
Results show that R-Zero is highly effective in enhancing the mathematical problem-solving performance of both families of LLMs.
The gains increase steadily over the iterations, but the largest boost occurs in the first round, which highlights the important role of the RL-trained Challenger. (Compare it with the results of the “Base Challenger” baseline as shown below.)
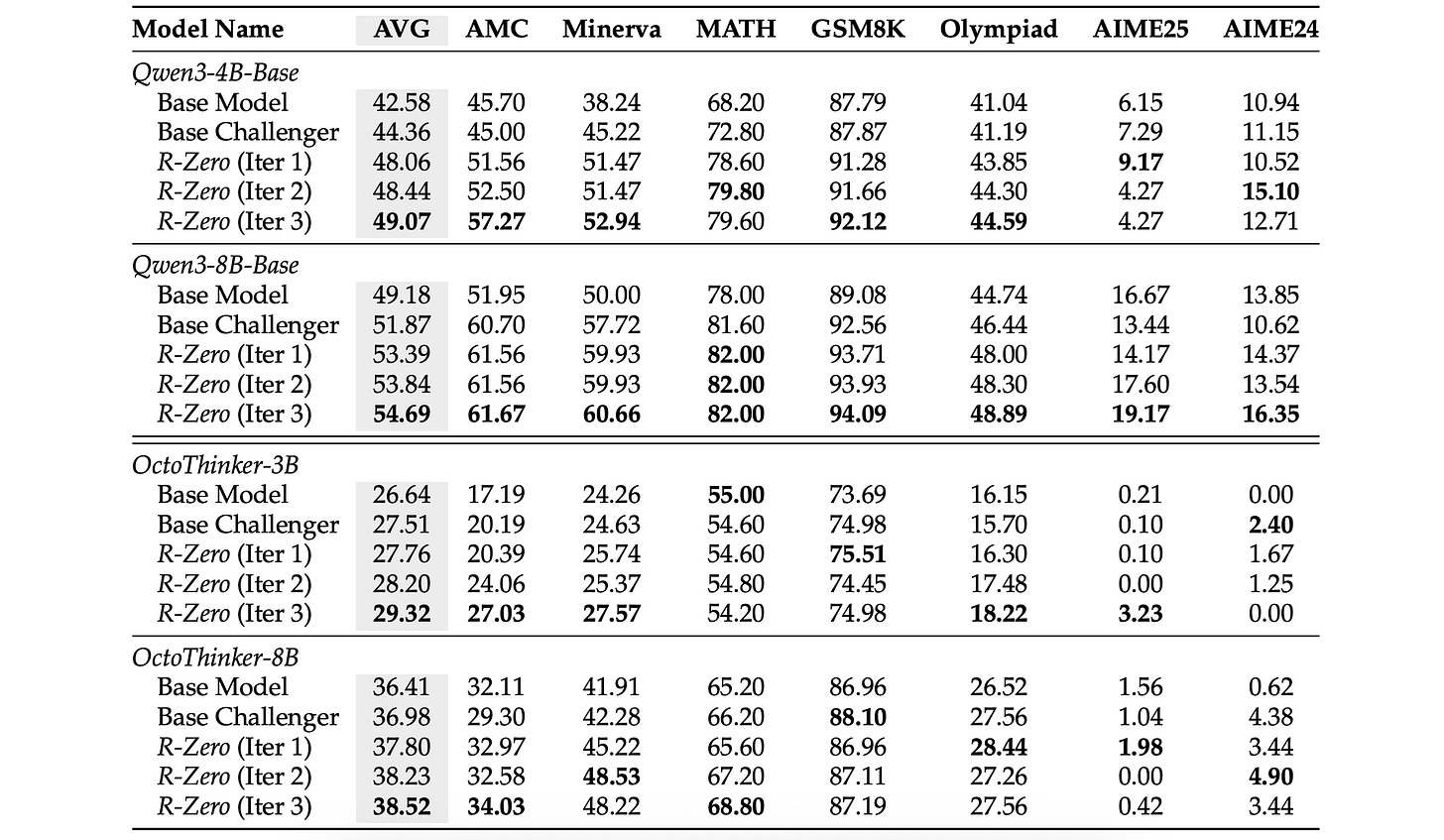
Even though R-Zero trains the LLM on mathematical reasoning tasks, the skills learned improve its general-domain reasoning performance as well.
This is seen in the table below, where such performance steadily improves across iterations.
R-Zero is an entirely autonomous framework that helps LLMs self-evolve to significantly improve their reasoning capability across multiple domains.
Although it currently focuses on mathematical reasoning, where correctness can be objectively verified, expanding it towards open-ended reasoning tasks would mean a way towards truly self-evolving LLMs.
I am excited for future work in this direction. What are your thoughts on it? Let me know in the comments below.
Further Reading
Research paper titled ‘R-Zero: Self-Evolving Reasoning LLM from Zero Data’ published in ArXiv
GitHub repository containing the code associated with the original research paper
Research paper titled ‘Learning to Reason without External Rewards’ published in ArXiv
Source Of Images
All images used in the article are created by the author or obtained from the original research paper unless stated otherwise.






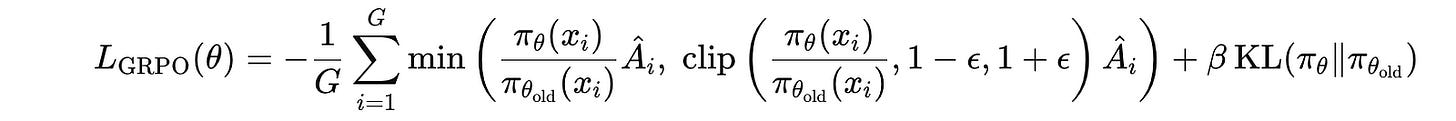
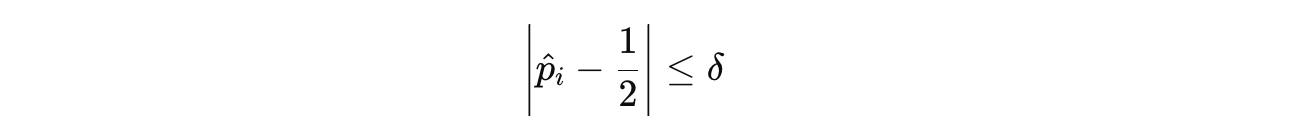


Great article and review thank you for sharing!