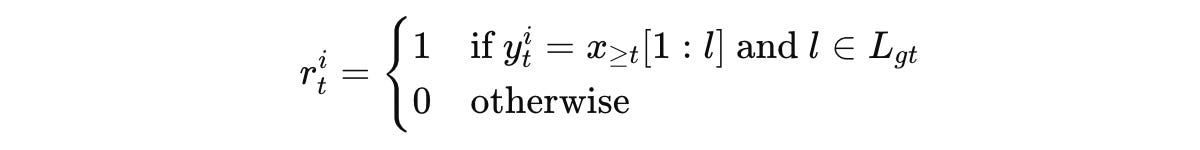LLMs Can Now Be Pre-Trained Using Pure Reinforcement Learning

A deep dive into Reinforcement Pre-Training (RPT), a new technique introduced by Microsoft researchers to scalably pre-train LLMs using RL.

Image generated with Google ImageFX

LLMs are conventionally pre-trained on large text datasets using the next-token prediction objective in a self-supervised manner.

Following their pre-training, they are fine-tuned for specific tasks using further supervised learning or alignment-tuned using reinforcement learning (RL).

However, this pipeline might not remain the de facto standard in the future.

A recent research paper by Microsoft has just introduced Reinforcement Pre-training (RPT), a new method of pre-training LLMs that reframes next-token prediction to a next-token reasoning objective.

Unlike conventional RL pipelines, this method does not use a reward model or any human-annotated training examples.

Instead, it uses an intrinsic reward based on how accurately the LLM in training predicts the next token from the training text.

Standard Next-token prediction objective used in LLM pre-training vs. Next-token reasoning objective introduced by Reinforcement pre-training (RPT)

Evaluations show that RPT is a very scalable approach to pre-training highly performant LLMs.

It leads to pre-trained LLMs with impressive zero-shot performance on various downstream tasks, which act as a great baseline for further improvements through RL fine-tuning.

This is a story in which we first discuss how LLMs are conventionally pre-trained and then deep dive into what Reinforcement Pre-training (RPT) is and how it challenges this conventional approach.

---

My latest book, called “LLMs In 100 Images”, is now out!

It is a collection of 100 easy-to-follow visuals that describe the most important concepts you need to master LLMs today.

Grab your copy today at a special early bird discount using this link.

---

To Begin With, What Is LLM Pre-Training?

Pre-training refers to the initial training of an LLM on huge text datasets using a self-supervised objective like:

• Next-token prediction (in the case of GPT) or

• Masked language modeling (in the case of BERT)

It helps an LLM learn general language patterns, grammar, vocabulary, world knowledge, and basic reasoning abilities.

Pre-training visualised (Image from author’s book “LLMs In 100 Images”)

Most currently popular LLMs are based on the GPT architecture, which uses the Next-token prediction objective, where the model learns to predict the next token in a sequence, given the previous tokens, during training.

Mathematically, for a given sequence of tokens x(0), x(1).., x(T) in the training datasets (where T is the total number of training tokens), the model is trained to maximise the following objective:

where:

• P(x(t) | x(0), x(1), …, x(t-1)) is the probability of obtaining the next token given the previous context x(<t)

• θ denotes the model parameters

Note that this objective is just the opposite (negative) of the Cross-entropy loss, which is minimised during LLM training:

Pre-training is usually followed by Post-training, where LLMs are commonly:

• Supervised fine-tuned to follow instructions (also called Instruction Tuning)

• Alignment-tuned to be helpful, safe and aligned with human values using Reinforcement Learning (with one of the methods called Reinforcement Learning with Human Feedback or RLHF)

• Trained to reason better using Reinforcement learning

SFT and RLHF visualised (Image from author’s book “LLMs In 100 Images”)

Although Reinforcement learning is very useful, it comes at a cost.

The conventional RL pipeline requires lots of human-label preference data to train a reward model, whose rewards direct the alignment of an LLM during training.

This, in turn, makes RL training prone to human biases.

The LLM in training can also get stuck hacking the reward-earning process without really improving its performance.

A fix was proposed with the introduction of Reinforcement Learning with Verifiable Rewards (RLVR) in a 2024 research paper on the Tulu 3 family of open-source LLMs.

RLVR replaces the subjective, human preference-based rewards with objective, rule-based, and verifiable rewards.

It requires a labelled dataset of question-answer pairs for training an LLM.

During training, the LLM (also called the Policy, a term commonly used in RL) generates a response given a question.

A verifier compares this response with the question’s corresponding answer (ground truth) and calculates a reward.

This reward is maximized during training based on the objective function as shown below (using a Policy gradient method like PPO or GRPO):

where:

• π(θ) is the LLM in training (Policy)

• θ denotes the parameters of the LLM in training

• (q, a) ~ D denotes a question–answer pair sampled from the dataset D

• o ~ π(θ)​(⋅ ∣ q) denotes the output o generated by the training LLM given the question q

• r (o, a) is the reward function that returns a reward based on how good the LLM output o is compared to the correct answer a .

In many cases, this reward function returns a binary reward (1 for a perfectly correct answer, and 0 otherwise).

The RLVR pipeline is shown in the image below.

RLVR visualised (Image from author’s book “LLMs In 100 Images”)

Now that we understand these two concepts well, it’s time to move ahead and learn about Reinforcement Pre-Training (RPT).

---

From RLVR To RPT

Reinforcement Pre-Training (RPT) takes the next-token prediction objective and changes it to the next-token reasoning objective.

Let’s understand what this means.

For a given sequence of tokens x(0), x(1).., x(T) in the training datasets (where T is the total number of training tokens), the LLM π(θ) is required to generate a Chain-of-Thought reasoning sequence c(t) before generating the next-token(s) prediction y(t), given the context x(<t).

(Note that y(t) is not necessarily a single token and can be a sequence of multiple tokens.)

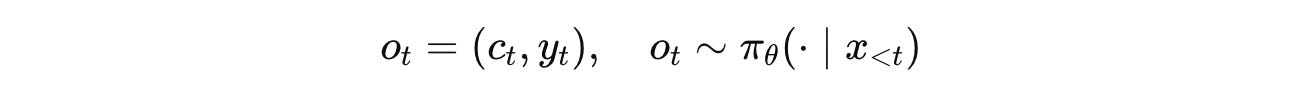
Output o(t) from the LLM/ Policy π with parameters θ is a combination of the Chain-of-thought reasoning c(t) along with the next token prediction y(t), given the context x(<t)

This approach changes the training text corpus into a big set of problems the LLM could reason on during training.

Standard Next-token prediction objective used in LLM pre-training vs. Next-token reasoning objective introduced by Reinforcement pre-training (RPT)

Training with next-token reasoning involves On-Policy Reinforcement learning, which means that the model in training improves based on the feedback (called “Reward” in RL) from its own outputs (called “Actions” in RL).

(This differs from Off-Policy Reinforcement learning, where a model could learn based on feedback from data generated by a different model.)

Let’s next discussion this RL process in detail.

For a given set of tokens x(0), x(1).., x(T) in the training datasets, for context x(<t), the LLM π(θ) generates G responses.

G responses generated by the LLM, each indexed by ‘i’

As previously discussed, each of the G responses denoted by o(t)(i) consists of:

• a Chain-of-Thought reasoning sequence c(t)(i) and

• a next-token prediction y(t)(i)

Hope things are clear till now. Let’s move forward to discuss the reward calculation process.

Similar to RLVR, each response receives a binary reward based on how correct the next-token(s) prediction y(t)(i) is compared to the ground truth answer/ completion x(≥ t).

Instead of directly comparing the tokens for reward calculation, these are first converted to byte sequences where:

• x̄(≥ t) denotes the byte sequences of the ground truth continuation/ answer

• ȳ(t)(i) denotes the byte sequences of the prediction, where l is its byte length

The set of the cumulative byte lengths that act as valid token boundaries in the ground-truth continuation x(≥ t) is given by L(gt).

(We will come back to this soon.)

Next, the reward for each response i (from the total G responses) is calculated using the following reward function:

This means that the reward is 1 when:

• the byte sequence of the prediction is an exact prefix of the ground-truth completion byte sequence, and

• its length l matches any valid token boundary

This reward is called the Prefix matching reward.

Let’s learn this all using an easy example.

Given the context x(<t) as:

“Electric force grows with charge”

And the ground-truth continuation x(≥t) as:

" size and decreases with distance squared"

Let’s say that the tokenizer splits them as:

“ size”, “ and”, “ decreases”, “ with”, “ distance”, “ squared”

The byte lengths and cumulative byte lengths of these tokens are as follows:

• “ size”: 5 bytes (cumulative: 5 bytes)

• “ and”: 4 bytes (cumulative: 5 + 4 = 9 bytes)

• “ decreases”: 10 bytes (cumulative: 5 + 4 + 10 = 19 bytes)

• “ with”: 5 bytes (cumulative: 5 + 4 + 10 + 5 = 24 bytes)

• “ distance”: 9 bytes (cumulative: 5 + 4 + 10 + 5 + 9 = 33 bytes)

• “ squared”: 8 (cumulative: 5 + 4 + 10 + 5 + 9 + 8 = 41 bytes)

These values make the set of valid byte-token boundaries, which is denoted by L(gt):

L(gt) = { 5, 9, 19, 24, 33, 41 }

These are the only lengths at which a predicted byte-prefix can cleanly end on a full token.

Now, let’s say that the LLM predicts the next-token sequences as:

• Response 1: “ size and” (byte length: 9 bytes)

• Response 2: “mass” (byte length: 4 bytes)

• Response 3: “ size a” (byte length: 7 bytes)

The reward function checks if:

• the model’s predicted byte sequence ȳ(t)(i) exactly matches the first l bytes of the ground-truth continuation x̄(≥ t)

• l is a part of L(gt)​ to make sure that the prediction stops cleanly at a token boundary (end of token), and not in the middle of a token.

If these conditions are true, the reward is 1. If either condition fails, the reward is 0.

For the next-token sequences predicted by the LLM in our example:

• “ size and” matches the first 9 bytes of the ground truth, and 9 is a valid token boundary, so the obtained reward is 1.

• “mass” does not match the start of the ground truth at all, so the obtained reward is 0.

• “ size a” again fails to match any of the conditions, so the obtained reward is 0.

Hope this example makes things clearer.

Given the context, predictions, and the ground truth completion, an LLM is trained to maximize the expected reward using the following objective function:

where:

• pairs of context x(<t) and ground truth continuation x(≥t) are sampled from the training text corpus (D)

• o(t)(i) are all the responses (total G, each indexed by i) generated by the LLM π with parameters θ

• r(t)(i) is the prefix-matching reward for each response/ LLM prediction

The complete RPT process is shown in the image below:

Illustration of Reinforcement Pre-Training (RPT). Each model response includes Chain-of-thought reasoning between <think>...</think> tokens, followed by the prediction enclosed in \boxed{}.

In short, what RPT does is it reframes the next-token prediction objective using RLVR, making RL easily applicable to Pre-training.

RPT reframes the Next-token prediction objective to the Next-token reasoning objective using RLVR

---

How Good Is RPT?

Researchers use Deepseek-R1-Distill-Qwen-14B as their base model and the OmniMATH dataset (consisting of competition-level mathematical problems) as the pre-training dataset for RPT.

The GRPO (Group Relative Policy Optimization) algorithm is used during training to maximise the RL objective, and the resulting pre-trained LLM is called RPT-14B.

GRPO visualised (Image from author’s book “LLMs In 100 Images”)

Here’s what the evaluation results on RPT-14B tell.

---

RPT Leads To An Impressive Language Modeling Performance

The tokens in the validation set from the OmniMATH dataset are first classified into ‘easy’, ‘medium’, and ‘hard’ categories based on how difficult they are to predict.

RPT-14B is then evaluated on this set against:

• Deepseek-R1-Distill-Qwen-14B: the base model for RPT-14B

• Qwen2.5–14B: the base model for Deepseek-R1-Distill-Qwen-14B

The results show that RPT-14B is more accurate at predicting the next token at all token prediction difficulty levels than the baselines.

RPT-14B outperforms both baselines across all test splits of the OmniMATH dataset

It is so good that its performance is comparable to a significantly larger reasoning model, R1-Distill-Qwen-32B (14B vs. 32B parameters)!

RPT-14B scores at par with R1-Qwen-14B/ 32B on average next-token prediction accuracy across all test splits of the OmniMATH dataset

---

RPT Has Promising Scaling Curves For Increasing Training Compute

Prior experiments have shown that the next-token prediction loss when pre-training LLMs follows a power-law decay with respect to the LLM size, training dataset size, and training compute.

This matches with RPT, which shows consistently improving prediction accuracy as training compute increases, following the power-law equation as below:

P(C) is the next-token prediction accuracy on the validation dataset, P*, α, and A are parameters to be estimated.

The increasing next-token prediction accuracy with increasing training compute is evident in the following plot for all subsets of the validation dataset.

RPT follows scaling laws with its next-token prediction accuracy increasing consistently with compute across all difficulty levels of the validation dataset. The high coefficient of determination (R²) tells how well the power-law function fits the observed accuracy data for different difficulty levels.

---

RPT Builds Better Foundations For Further RL Training

After pre-training, when the base model (R1-Distill-Qwen-14B) is continually trained using the next-token-prediction objective on the same data used for RPT (but without RL), this harms the reasoning ability of this model.

Its accuracy drops from 51.2% to 10.7% and further fine-tuning with RLVR does not improve it much.

On the other hand, when RPT-14B is fine-tuned with RLVR on selected challenging questions via the Skywork-OR1 pipeline, it achieves higher next-token prediction accuracy both before and after the RLVR fine-tuning.

RPT-14B has a higher next-token prediction accuracy both before and after RLVR fine-tuning compared to the baseline.

This suggests that RPT actually builds strong reasoning patterns, which can be improved with further RL as compared to pre-training with next-token prediction (which might be making an LLM memorise training data without truly understanding it).

---

RPT Leads To An Amazing Zero-Shot Performance On General-Domain Tasks

When evaluated on two general domain benchmarks:

• MMLU-Pro: a multi-task language understanding benchmark

• SuperGPQA: a benchmark with graduate-level reasoning questions from 285 disciplines

RPT-14B has better zero-shot performance as compared to both R1-Distill-Qwen-14B and the much larger R1-Distill-Qwen-32B in the settings shown below.

RPT-14B in reasoning mode consistently outperforms the R1-Distill-Qwen-14B/ 32B baselines.

---

But How Does RPT Work So Well?

To answer this question better, researchers study the thought processes of the two models, R1-Distill-Qwen-14B and RPT-14B, on problems from the OmniMATH dataset.

The reasoning patterns are grouped into 6 categories based on the keywords in the model responses:

• Transition: where the model switches reasoning strategies

• Reflection: where the model checks its own reasoning assumptions

• Breakdown: where the model decomposes the problem into smaller parts

• Hypothesis: where the model proposes and tests possible outcomes

• Divergent Thinking: where the model explores multiple possibilities

• Deduction: where the model draws logical conclusions from given information

The following keywords help identify these reasoning patterns.

Keywords and their corresponding reasoning pattern groups

The analysis tells that RPT-14B’s reasoning is significantly different from the baseline.

RPT-14B uses the ‘Hypothesis’ pattern 162% more and the ‘Deduction’ pattern 26.2% more than R1-Distill-Qwen-14B which relies heavily on the ‘Breakdown’ pattern.

This suggests that RPT-14B has a deeper, inference-driven reasoning style compared to the conventional, structured step-by-step problem-solving approach.

RPT-14B shows a higher use of ‘Hypothesis’ and ‘Deduction’ patterns when reasoning as compared to the baseline (R1-Distill-Qwen-14B)

An example of RPT-14B’s thinking process is shown below, where it thinks through the context and reasons deeply when answering rather than relying on superficial pattern matching.

An example of the thinking process of RPT-14B

---

The experiments in the research paper were conducted using a 14B parameter model, with the pre-training dataset consisting solely of mathematical problems.

It would be interesting to know how well RPT performs when applied to training on general-domain text with a larger model and higher training compute.

Given its impressive performance in these evaluations, RPT is still a very promising method for pre-training LLMs, in my opinion.

What are your thoughts on it? Let me know in the comments below.

---

Further Reading

• Research paper titled ‘Reinforcement Pre-Training’ published in ArXiv

• Research paper titled ‘Tulu 3: Pushing Frontiers in Open Language Model Post-Training’ published in ArXiv

• Research paper titled ‘Training language models to follow instructions with human feedback’ published in ArXiv

• Research paper titled ‘DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning’ published in ArXiv

• Research paper titled ‘Quiet-STaR: Language Models Can Teach Themselves to Think Before Speaking’ published in ArXiv

---

Source Of Images

All images used in the article are created by the author or obtained from the original research paper unless stated otherwise.

---

Subscribe to ‘Into AI’ — a newsletter where I help you explore the best and latest in Artificial Intelligence from the ground up by dissecting the original research papers.