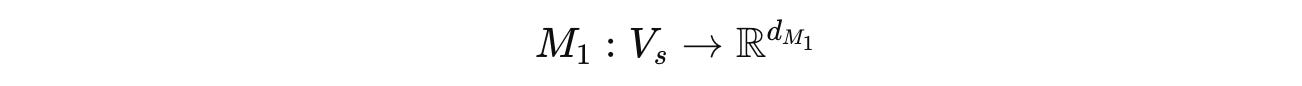Your Vector Databases Aren’t Safe Anymore

A deep dive into the ‘Vec2Vec’ method that can translate embeddings from unknown encoders and decode them to extract sensitive information about a Vector database.

Jun 02, 2025

Embeddings are the secret sauce of Deep learning.

While you and I can make sense of at most 3 dimensions, LLMs like ChatGPT can think in 2048 or more dimensions.

During training, LLMs learn an embedding matrix that maps a given word (token) ID to a higher-dimensional vector (embedding).

The magical part is that when text is converted into embeddings, its semantics stay intact.

In other words, two words/ sentences with similar meanings create embeddings that lie very closely in a higher-dimensional space.

Embeddings visualised (Image from author’s book titled “**AI In 100 Images**”)

Vector databases use this exact property of embeddings.

They are collections of document embeddings created using an Encoder or Embedding model.

This collection of embeddings can later be searched for in view of similarity to a given query.

Embeddings created by different embedding models are quite distinct.
In other words, their vector spaces do not match.

But what if we could somehow ‘translate’ these distinct embeddings created by different embedding models into a single universal vector space to compare and even decode them?

Researchers from Cornell University have just made this possible using their method called ‘vec2vec’.

This method can transform embeddings from unknown embedding models into a common vector space and decode them from there to extract sensitive information from the documents that made up these embeddings.

As shown in the image on the left, T5-based and BERT-based embeddings are not comparable. Vec2Vec transforms them and represents them in a common vector space, which allows them to be compared.

Here is a story where we deep dive into how ‘vec2vec’ works, how it was trained, how effective it is, and why it is such a big security threat for all vector databases used today worldwide.

But First, A Little Diversion Into The Philosophy Of Plato

(This diversion is important to understand what we discuss in the upcoming sections. Trust me on this.)

Plato, an ancient Greek philosopher, in his Theory of Forms, described the concept of ideal reality.

He believed that the physical world we see is not the true reality.

Instead, true or ideal reality lies beyond the physical world, in the form of perfect, eternal, and unchanging Forms or Ideas.

Our physical world is just an imperfect and temporary shadow of these ideal Forms.

For example, all the beautiful things we see in our world reflect an ideal Form of beauty that is perfect and timeless. Similar Forms exist for other qualities as well.

Now, how does this relate to Machine learning, you’d ask?

Plato’s theory appealed to many ML researchers, who suggested that a similar version existed for deep learning neural networks.

As larger neural networks are trained on bigger and more diverse datasets, their internal data representations converge.

This is the case even when they are trained on different datasets and modalities, with different training objectives and network architectures.

It is as if an ideal, shared statistical model of reality exists for these neural networks, which they all approximate towards.

This idea is known as the Platonic Representation Hypothesis for deep neural networks.

The Platonic Representation Hypothesis states that image X and text Y are projections of a common underlying reality Z. Although f(img) and f(text) produce different embeddings for these two modalities, they come from the same shared representational state Z.

Cornell researchers further extend the Platonic Representation Hypothesis by proposing that the ideal reality, or the universal latent structure of data representations, can be learned.

Currently, different embedding models create results that are in completely different vector spaces.

But once this universal structure is learned, one could translate different representations from one vector space to another without knowing about the data or the encoders used to create them.

Let’s learn how this is done.

Here Comes ‘Vec2Vec’

Suppose we have a collection of document embeddings available from a compromised vector database, as shown below:

Each of these vectors u(i) is created using an unknown embedding model/ encoder M(1), applied to unknown documents d(i).

What the encoder does is map from a source document space V(s) to a vector space of dimension d(M(1)).

Next, suppose we have access to a different encoder M(2) that maps from the source document space V(s) to a different vector space of dimension d(M(2)).

Assuming that the documents contain text in English, we need a function F that can ‘translate’ the compromised document embeddings u(i) into the output vector space of M(2).

This function F is implemented using the ‘vec2vec’ model, and its goal is to produce translated embeddings v(i) as close to the ideal embeddings that would be produced if the original text documents were directly embedded using M(2).

where:

Once this is done, and given that we have access to M(2), we could apply previously known Embedding inversion/ inference methods to reconstruct the original text documents from their compromised embeddings.

Vec2vec generates a translation function F that acts on document vector embeddings u(i) to approximate the ideal embeddings v(i) without having access to the encoder M(1) or the original text documents d(i) used to create document vector embeddings u(i)

A Deep Dive Into The Architecture Of ‘Vec2Vec’

‘vec2vec’ is based on the Generative Adversarial Network (GAN) architecture.

If you’re new to a GAN, it consists of two neural networks:

Generator (G) that tries to generate data that resembles real data
Discriminator (D) that tries to distinguish between real data and fake data from the Generator

These networks are trained using a minimax two-player game played between them.

During training, the Generator improves by trying to fool the Discriminator, and the Discriminator improves by correctly detecting fakes produced by the Generator.

Adapted from GANs, ‘vec2vec’ consists of the following components:

Input adapters A(1) and A(2) that transform embeddings from the vector spaces of encoders M(1) and M(2) into a shared universal latent vector space with dimension Z

Shared backbone T that learns the universal latent space (of dimension Z) where the different embeddings can be aligned

Output adapters B(1) and B(2) that transform the shared universal latent vector space into the specific vector output space of the encoders M(1) and M(2)

The functions F(1) and F(2) translate embeddings from the space of the encoder M(1) to M(2) and vice versa, respectively.

The functions R(1) and R(2) takes an embedding from the encoders M(1) and M(2), pass them through the universal latent space, and return a reconstructed version in the same original embedding space.

These four functions make up the Generator network, which is trained to produce embeddings that look real (to fool the Discriminators).

Next, four functions form the Discriminator network:

D(1): distinguishes real vs. translated embeddings from M(1)
D(2): distinguishes real vs. translated embeddings from M(2)
D(1)(l): distinguishes whether a latent vector came from M(1)’s embedding via A(1)
D(2)(l): distinguishes whether a latent vector came from M(2)’s embedding via A(2)

Generators are Multi-layer Perceptrons (MLPs) with residual connections, layer normalization, and SiLU activations.

Discriminators have architectures similar to Generators but do not have residual connections to ensure stability during training.

These components and the overall pipeline are shown in the image below.

Given a vector database containing embeddings from an unknown encoder (Encoder A), Vec2vec can transform them into the vector space of a known embedding model (Encoder B). The translated embeddings can then be used to reveal information about the original documents in the vector database.

How Is ‘Vec2Vec’ Trained?

All model parameters together (θ) are trained by balancing two objectives as follows:

Joint adversarial minimax training of Generators and Discriminators, where L(adv) and L(gen) are the Adversarial and Generator losses, respectively, and `λ(gen) controls their balanace`

These objectives are:

Adversarial Loss L(adv) that ensures generated embeddings match the distribution of real embeddings in both the target and latent spaces.

The adversarial objective L(adv) is the sum of two GAN losses: two for translating between embedding spaces (the first two terms in the equation RHS) and two for aligning their latent representations (the last two terms in the equation RHS)

Generator loss L(gen) that consists of three constraints that preserve the semantics of the embeddings.

These constraints are as follows:

Reconstruction Loss (L(rec)) which minimises distortion when embeddings are mapped to the latent space and back to their original space.

Reconstruction loss is the expected squared error between original embeddings and their reconstructions in the spaces of both encoders M(1) and M(2). x and y are embedding vectors produced by encoders M(1) and M(2), respectively, and p and q are the corresponding data distributions over those embeddings.

Cycle-Consistency Loss (L(CC)) which ensures that translating an embedding to another space and back preserves the original embedding.

Cycle‐consistency loss measures the mean squared error between each original embedding and its reconstruction after translating it to the other encoder space and back.

Vector Space Preservation Loss (L(VSP)) which maintains pairwise relationships between embeddings after translation.

For a batch of B embeddings, Vector Space Preservation Loss is the average squared difference in the pairwise inner-product similarities resulting from translations by F(1) and F(2).

The total generator loss L(gen) combines all of these, with the λ terms weighing each constraint, as follows.

If this seems too complex to understand, here is how it can be simply put:

During training, Discriminators aim to better differentiate real from generated embeddings by maximizing the L(adv).
Generators on the other hand, aim to fool the Discriminators and preserve the embedding structure, and do so by minimizing L(adv) + λ(gen) L(gen).

Is ‘Vec2Vec’ Really That Good?

‘vec2vec’ is trained on two sets of embeddings generated from disjoint sets of 1 million 64-token-long sequences from the Natural Questions (NQ) dataset of user queries and Wikipedia-based answers.

A part of this dataset is used for evaluation, alongside the following evaluation datasets:

TweetTopic: A dataset of multi-labelled tweets
MIMIC: A medical dataset (subset of MIMIC-III) containing patient records labelled with MedCAT disease descriptions
Enron Email Corpus: An unlabelled dataset of internal emails from the defunct energy company, Enron

The following embedding models are used in the experiments.

Results show that ‘vec2vec’ is very effective in learning the universal latent vector space and translating the embeddings into it, even when they look dissimilar in their original form.

Pairwise cosine similarity between original embeddings and their vec2vec translations/ latents

When ‘vec2vec’ is trained and tested on text from the same data source (in-distribution translation), the translated embeddings almost perfectly match the target ones (cosine similarity scores up to 0.92 and top-1 accuracies up to 100%).

Similar results are seen in out-of-distribution translation performance (when it is trained on a text from a data source but tested on another), which tells that it can generalise well to new topics/ text domains and is not tied to a specific dataset.

‘vec2vec’ is not just limited to text encoders, but it can translate embeddings to and from the vector space of CLIP, a multi-modal embedding model trained on both text and images.

While the results are not as amazing as purely text-based models, it achieves a cosine similarity of up to 0.78 and top-1 accuracy of up to 0.72 when translating between CLIP and text models.

This shows that it is highly adaptable to new modalities since CLIP embeddings have been successfully connected to other modalities (heatmaps, audio, and depth charts) in a previous research work.

How Are ‘Vec2Vec’ Translations Decoded?

Researchers use two ways to decode information about the original documents given the embeddings.

Zero-shot attribute inference: This is a zero-shot technique where a vec2vec-translated embedding is compared for cosine similarity to the embeddings of different attributes (names, topics, labels, etc.), and the top-k most similar attributes are picked.
Zero-shot inversion: This technique reconstructs texts given the embeddings and the embedding encoder in a zero-shot fashion (without training on ‘vec2vec’ outputs).
Its details are found in the ArXiv research paper titled ‘Universal Zero-shot Embedding Inversion’.

‘vec2vec’ embeddings perform well with zero-shot attribute inference on multiple evaluation datasets, including the one with medical records (MIMIC).

They can be surprisingly inferred for rare disease terms like ‘Alveolar Periostitis’, which have never appeared in vec2vec’s training data!

For zero-shot inversion, which is more difficult than attribute inference, information can be extracted for around 80% of documents given their vec2vec-embeddings.

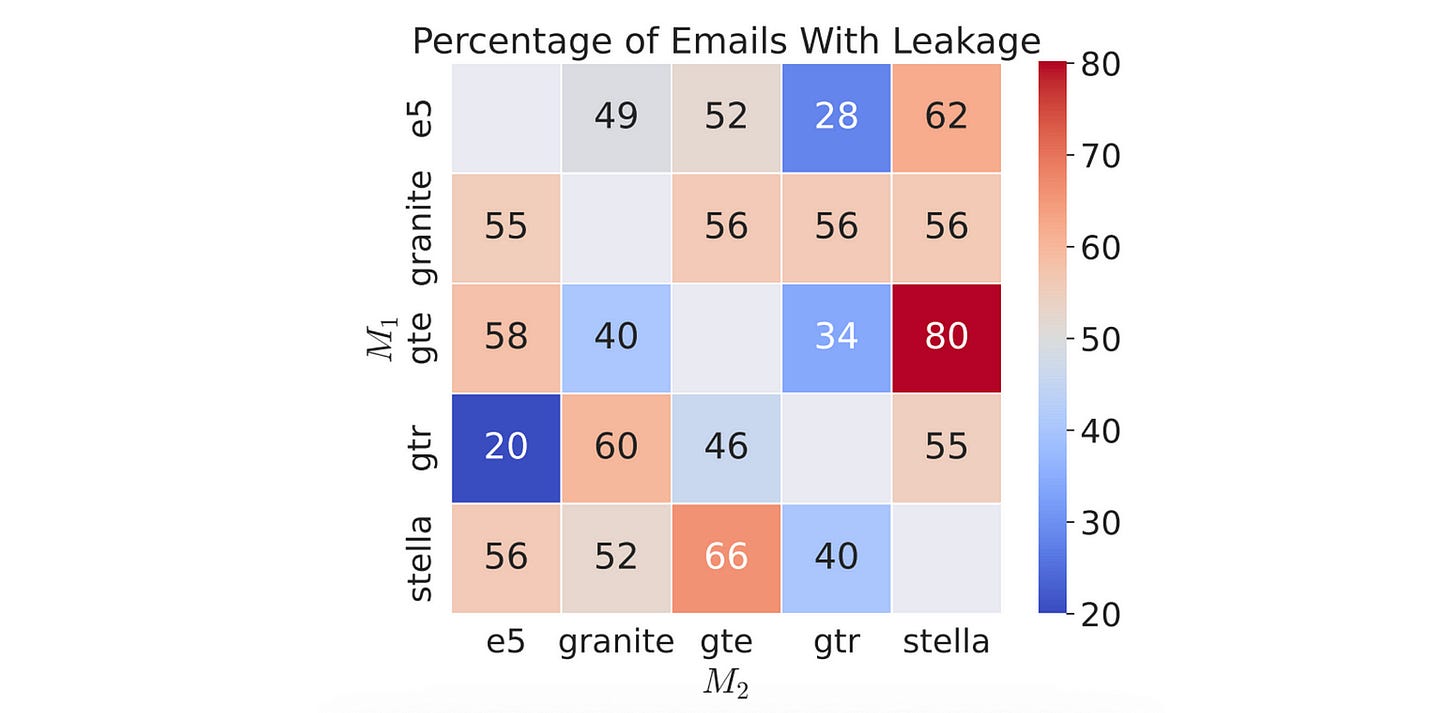
LLM-as-a-Judge accuracy (using GPT-4o as a judge) for leakage of information via zero-shot inversion for vec2vec embeddings trained on the Natural Questions (NQ) dataset and evaluated on the Enron Email Corpus dataset

Although not perfect, the inversion method can impressively extract meaningful information such as individual/ company names, dates/ promotions, financial data, outages and even lunch orders!

Zero-shot inversion reveals entities (shown in green) and content (shown in yellow) from vec2vec embeddings.

‘vec2vec’ is super-impressive, and I feel that its performance will improve over time, over multiple modalities, as it learns to predict the ultimate and ideal reality for all deep learning neural networks.

Now is the time to guard your vector databases in the best possible way than ever before.

They aren’t as secure as we thought they were.

Source Of Images

All images used in the article are created by the author or obtained from the original research paper unless stated otherwise.

Subscribe to ‘Into AI’ — a newsletter where I help you explore the best and latest in Artificial Intelligence from the ground up by dissecting the original research papers.

Into AI