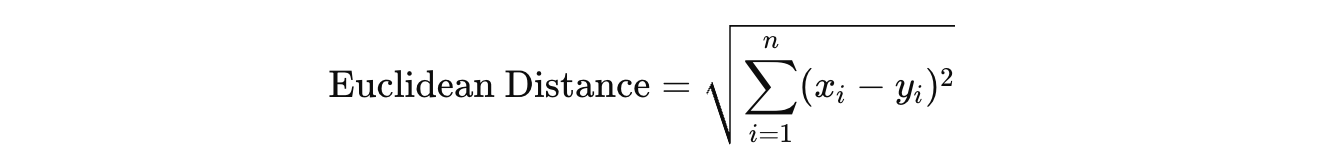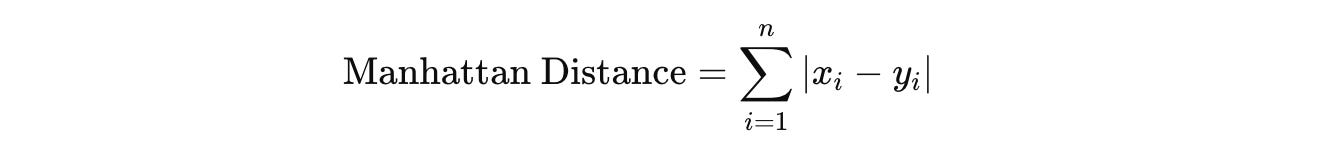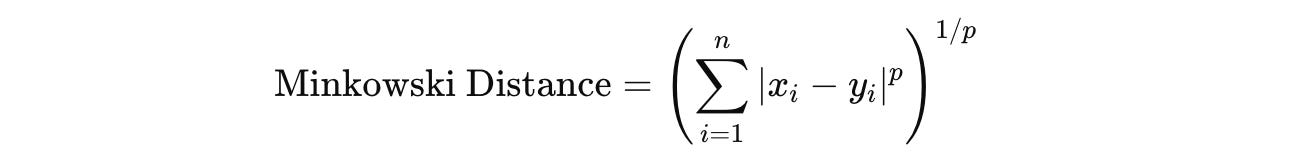ML Interview Essentials: K-Nearest Neighbours (KNN)

#4: Learn to build K-Nearest Neighbours (KNN) from scratch in Python (9 minutes read)

👋🏻 Hey there!

This article is a part of the ‘ML Interview Essentials’ series on the publication.

If you have not read the previous articles in this series, here is your chance to get interview-ready like never before.

ML Interview Essentials: Building Self-Attention From Scratch

ML Interview Essentials: What Is Normalization?

ML Interview Essentials: What Is Gradient Descent

Let’s begin!

---

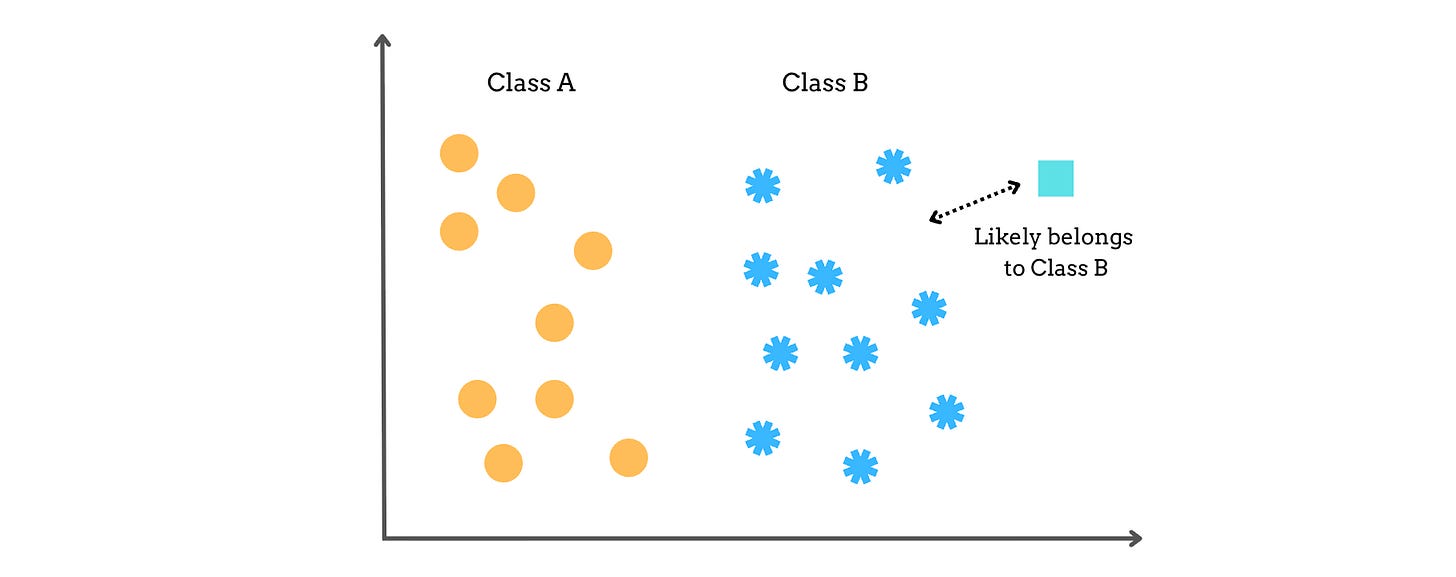
K-Nearest Neighbors (KNN) is a supervised learning algorithm primarily used for classification problems (though it can also be used for regression).

KNN works based on the assumption that data points that are close to each other in the feature space are likely to belong to the same class.

Therefore, a given new data point will belong to the class with the closest data points to itself (called ‘neighbors’).

For regression tasks, a new data point will get the average values of its closest neighbors.

The algorithm is:

• Lazy (Non-eager): because it does not have a traditional training phase like neural networks, and it simply does all computation during the prediction phase

• Non-parametric: because it makes no assumptions about the underlying data distribution and predicts based on stored data points rather than learned parameters

• Computationally expensive: because it must search through all stored training points to find the K nearest neighbors at prediction time.

---

Steps In The KNN algorithm

1. We begin by choosing the number of neighbors (K), a hyperparameter, before running the algorithm.

2. Next, for a new data point (test/ query datapoint), KNN calculates the distance between it and the existing data points in the training dataset.

   
   Various distance metrics can be used in this step, including:

   • Euclidean distance or L2 Norm

   • Manhattan distance or L1 Norm

   • Minkowski distance

   
   We will discuss these metrics in detail in the next section.

3. After calculating the distances, all points in the training dataset are sorted by their distance to the query datapoint, and the top K closest matches are selected.

4. Finally, when used for a classification problem, the class that appears most frequently among these K neighbors is assigned to the query datapoint (by majority voting).
   When used in a regression problem, the average value of the K neighbors is assigned to the new data point.

---

More On Distance Metrics

Various metrics can be used to measure the distance between a test data point and the training dataset’s existing data points.

Here are three important ones that you need to know about:

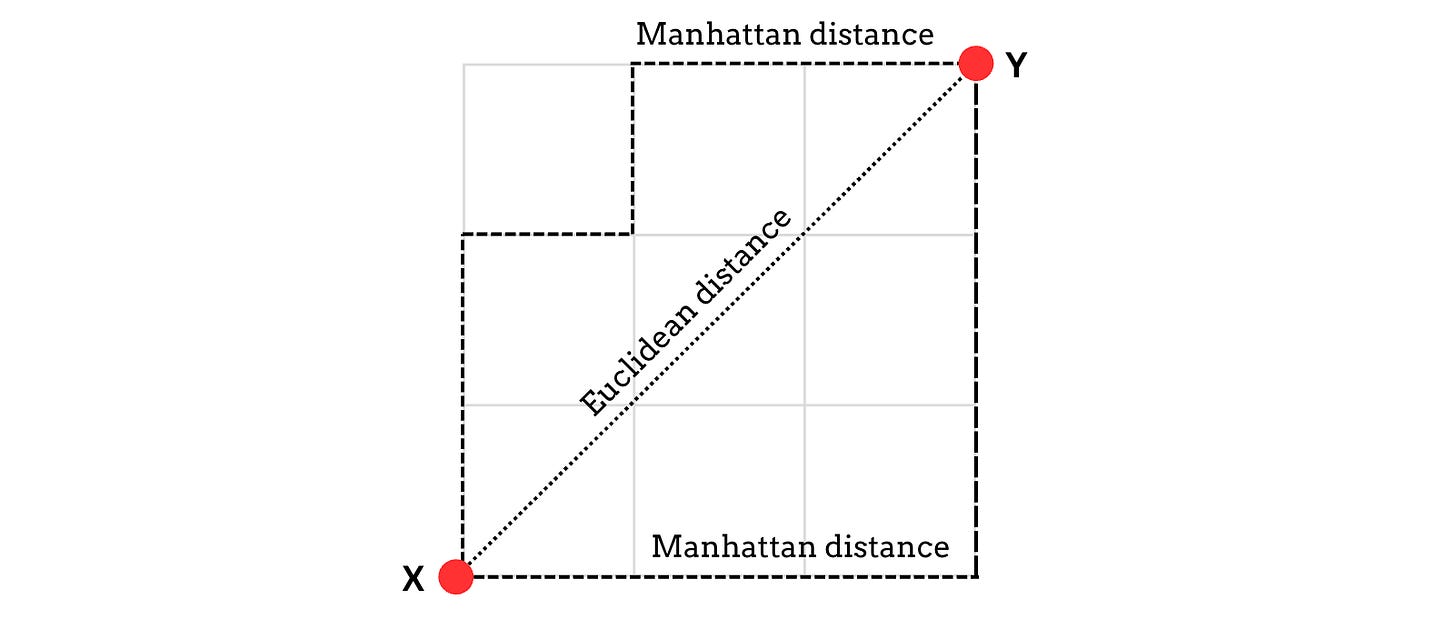
1. Euclidean Distance (also called L2 Norm): This is the measure of the straight-line distance between two points in Euclidean space.

   In all distance formulae shown below, x(i) and y(i)​ represent the i-th dimension of the two points x and y, and n is the total number of dimensions.

2. Manhattan Distance (also called L1 Norm or Taxicab Distance): This is the measure of the distance between two points in a grid-based path, calculated as the sum of the absolute differences of their corresponding coordinates.

3. Minkowski Distance: This is the measure of the distance between two points by taking the p-th root of the sum of the absolute differences of their coordinates raised to the power p.

   

   Its special cases are the Euclidean and Manhattan distances.

   • When p = 1, the formula represents the Manhattan distance.

   • When p = 2, the formula represents the Euclidean Distance.

These distances between the points x and y are better understood graphically, as shown below.

The Euclidean distance between points x and y is 3 units, whereas the Manhattan distance between them is 6 units.

---

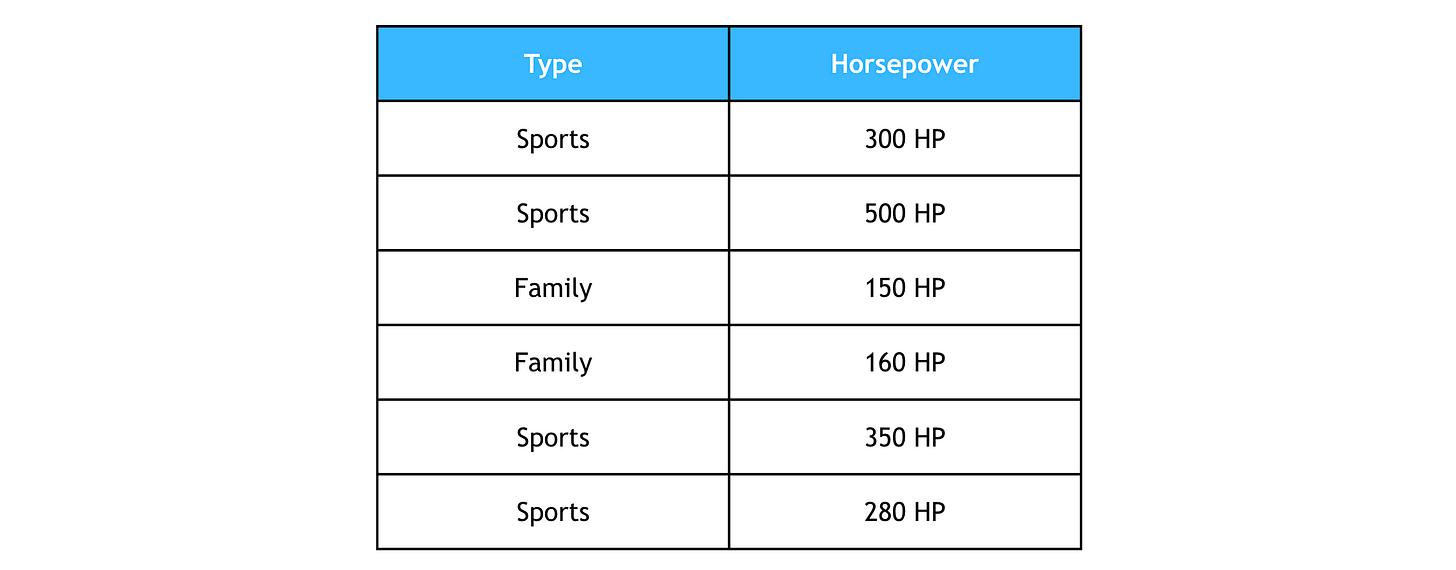
KNN For Classification: Classify Cars At A Dealership

Let’s say we have a dataset of cars available at a dealership. Each car has a horsepower value and belongs to one of two categories: Sports or Family.

Given an incoming car of 250 horsepower, we want to classify it into one of these types.

Step 1: Set K to 3, which means considering three nearest neighbours in KNN calculations

Step 2: Calculate the Euclidean distances between the new data point (250 horsepower) and all other data points in the dataset.

• To Sports Car 1 (300 HP): √(250 - 300)² = √2500 = 50

• To Sports Car 2 (500 HP): √[(250 - 500)² = √62500 = 250

• To Family Car 1 (150 HP): √(250 - 150)² = √10000 = 100

• To Family Car 2 (160 HP): √(250 - 160)² = √8100 = 90

• To Sports Car 3 (350 HP): √(250 - 350)² = √10000 = 100

• To Sports Car 4 (280 HP): √(250 - 280)² = √900 = 30

Step 3: Sort by distance and find the three nearest neighbours (since K = 3) to the new datapoint.

• Distance to Sports Car 4 (280 HP) = 30

• Distance to Sports Car 1 (300 HP) = 50

• Distance to Family Car 2 (160 HP) = 90

Step 4: Among the top 3 nearest neighbours, the ‘Sports car’ class receives two votes, while the ‘Family car’ class receives one vote.

This means that the incoming car of 250 HP belongs to the ‘Sports car’ class.

---

KNN Classifier In Python

It’s time to write some code.